数学学习方法整理
Table of contents
- 1 前言
- 2 基本方法
- 3 数学笔记
- 4 数学证明与推导
1 前言
本文整理了我近几年关于数学学习方法与如何记笔记的想法与实践。虽然我也并未百分百地做到了预想的方式与状态,但是能够藉此机会时常回顾、总结、反省,引发更多对于学习方法的思考,并带来一些心态上的方向性引导。同时,当经历了一段时光后,再回首纵观整个演变历程,则有助于形成和改进对自我的整体认识,从而不忘初心与至善目标。
2 基本方法
2.1 数学学习的态度、方法、策略(08/12/18)
-
Make mathematics study a habit with dogged perseverance
-
Don’t build mansion on top of loose sand. Concrete a solid foundation by allocating at least one hour for math study every day to make it a habit like reciting English words. Morning time after you getting up is recommended, during which you are facing least interruptions, your mind has its prime status and your mood is most optimistic.
-
Study math in focused mode by adopting the conception of deep work.
-
Interweave studying new knowledge and reviewing old knowledge (from which new understandings can be obtained). Interweave multiple topics from different sources to prevent Einstellung.
-
-
When facing difficulties
-
Don’t stuck in one book or paper. Compare materials on the topic from different sources to find clues and hints.
-
Don’t stuck at the topic or problem for too long time. Circumvent it and progress forward. This is similar to practicing flute: playing a segment or a piece all the time is not recommended, during which the initial mindful action will gradually degrade to mechanical repetitions.
-
Overconfidence about your wisdom and creativity to grapple with the problem without asking anyone or referring to any materials is a bad habit. It wastes too much time with little harvest. Just be humble to learn from others. Ask questions on a forum and don’t be shy or afraid of trouble and inconvenience.
-
-
Use the problem solving approach
-
Doing exercises is an indispensable measure to achieve a real understanding and final mastering of the knowledge.
-
A certain amount of exercises are mandatory for both deepening your understanding and making you proficient in applying mathematical concepts and techniques. However, there is no need to complete all the exercises if you are not going to publish a book on the whole exercise collection.
-
Be brave, open and confident to apply the learned mathematical concepts and techniques to problems in real world. Any success or even financial income derived from such competent or irreplaceable work will produce positive feedback on your diligent and perennial study. Furthermore, you may discover new meanings from it besides the pure and sublime beauty of the mathematical edifice with its rigorousness and delicacies.
-
2.2 输出型学习
2.2.1 输入型与输出型学习的一般方法(09/10/18)
在将数学笔记整理为幻灯片的过程中时常发现,虽然我之前已经认真地写下了详细的笔记,可仍有不少需要修改和完善的地方。例如,逻辑上存在不严谨之处,行文不够流畅完美。这些问题在一个人闷头学习(即输入型学习)的时候尚不易察觉,而当想要给别人讲解传授(即输出型学习)时,因为不允许有任何瑕疵、错误和逻辑环节的缺失,它们便自然地浮出水面,不得不予以正视、更正和完善了。
仔细想来,上述现象也许是由于输入型学习和输出型学习之间的差异所导致的。在输入型学习的时候,由于已经掌握了可以前后呼应、参照的大量信息,所以即便有思维和逻辑上的跳跃乃至一定的缺失,对于正确结论的获得也并不会有太大的影响。另一方面,在自我的封闭系统中以被动接受信息的方式学习,也容易因为存在思维上的死角,以及由浮躁、骄傲、急功近利产生的自以为是,而觉得已经了解了一切——可事实却往往远非如此。这样一来,虽然在输入型学习的过程中也认真地做了笔记,但是命题的阐述和推演的过程亦难免存在被自己忽视的瑕疵。定义、定理、结论、讨论在笔记中呈现的次序也不完全符合在输出型学习即讲解传授的情况下所应严格遵循的由已知到未知、由浅入深、循序渐进的一般顺序。
与此同时,我们也可以发现,输入型学习的模式是跳跃的、非线性的,而输出型学习的模式是连贯的、线性的。这是因为在后者的模式下,学习者需要以虚拟的授课者身份面对潜在的听众,从而必须事先对知识的组织方式和编排次序反复推敲,才能最终实现如链条环环相扣般的连贯而线性的呈现。这也就是我们常说的将知识的脉络一一理顺,使之各得其所。如果做不到这一点,我们便很难说这个学习者真正透彻地理解了知识。而若此人今后有机会成为老师,估计也只会是他/她自己讲得津津有味,而令学生云里雾里。
总的来说,积极主动的输出型学习对逻辑严谨性、完整性和准确性提出了比传统被动的输入型学习更高的要求。除了大家已经公认的反复练习与实践外,输出型学习对于个人牢固与深刻地掌握所学知识亦具有不可或缺、不可替代的作用。
2.2.2 数学的输出型学习方法(04/16/18)
今天早上在学习James Munkres《拓扑学》的时候想到,为了能够在数学方面达到较为专业的水平,必须要同时在基础理论和创新性上下功夫。对于纯数学的创新性,自己目前尚无能为力。但在基础理论方面,则仍旧大有文章可做。比如,
-
完全可以像国外数学系老师在其个人网站上做的那样,提供
-
相对于书本更为详细的证明和形象的解释的讲义或者笔记,
-
提纲挈领、循序渐进,从而适合初学者的幻灯片。
-
-
适用Freeplane制作数学思维导图,呈现各个定义、定理等知识点的组织架构和脉络联系。
-
更进一步地,制作讲解视频或者带有动画的网页文稿。即,实现数学的可视化。
为此,需要在数学基础理论的扎实学习、信息整理和组织上下功夫,持续积累。目前可以做的是,从正在学习的《拓扑学》、《实分析》、《泛函分析》等科目开始,
-
将有(1)难度的;(2)有逻辑环节缺失的;(3)缺乏形象的可视化图示甚至动画的定理、命题、引理、推论的证明过程追加上自己的注解和评述,重新组织和整理出文章,放到博客中。这些内容积少成多后,可以形成自己的讲义 。
-
给出所有课后习题的解答,放到博客文章中。这些内容积少成多后,可以形成自己的习题集 。
-
提炼讲义内容,填入必要的背景知识和阐释,使其成为适合初学者的幻灯片 。
-
定理、命题、引理、推论以及课后习题中出现的结论组织到思维导图 中。
为了给自己设定明确的目标和评价的指标,需要有deliverables。为此,目前暂定每周至少总结出两片博客文章。试运行一段时间后,再酌情增加或者减少。
所有科目的目录:
- James Munkres《拓扑学》
- Royden《实分析》
- Royden《泛函分析》
- Yosida《泛函分析》
- Sobolev Spaces
- Differential geometry
2.3 总结、实践、内化数学知识(11/04/20)
- 核心思想:将知识内化,真正理解,才能够真正记住。
- 改进方法
- 广泛、细致、深入地学习教材、阅读文章,丰富自己的骨架、工具箱、弹药库。
- 使用Workbook进行笔记的快速记录与整理,加入自己的批注。在Workbook里可以以最高的效率自由书写,不用顾及笔迹与卷面。
- 在正式的笔记本上整理相对正式的笔记。须知,即便将其完成,它们也绝非sacrosanct而一承不变。而是随时可以涂改、修订与完善的。要让笔记充分地发挥其应有的作用,而不能只是一件漂亮的摆设。
- 寻找与构造适合自己的证明的表述方法。
- 用属于自己的、叙述性的、精确的、概括性的语言来重述定理的证明过程。
- 用示意图形象地展示证明过程中的关键环节。
- 寻找或构造具体的例子将抽象与现实世界相关联。
- 寻找或构造反例对定理有全面、深入的把握。正所谓“叩其两端而竭焉”(《论语·子罕篇第九 9.8》 子曰:“吾有知乎哉?无知也。有鄙夫问于我,空空如也。我叩其两端而竭焉。”)。
2.4 数值算法从理论到实践的三种工作模式(10/11/21)
在将数值算法从理论转化为最终代码的过程中,我逐渐发现需要在如下三种工作模式间进行适当与及时的切换。否则,便容易在不自觉中将一种模式下的思维方式、工作方法、状态习惯部分地带入到另一种工作模式下,从而导致效率低下、收效甚微。
- 理论推导:细致入微,寻根究底,不放过证明中的每一个逻辑环节。
- 设计构思:在稿纸或白板上展开头脑风暴,在宏观层面关注数据结构、功能模块的组织,兼顾编程实现的便捷性与算法的性能。
- 代码开发:将任务分解至最细的粒度,精雕细琢,逐一完成。此时,不必在意逻辑的严谨与证明过程的完整,以拿来主义的方式直接将理论结果转为代码。
3 数学笔记
3.1 手写笔记符号(01/04/15)
3.1.1 条目标记符号
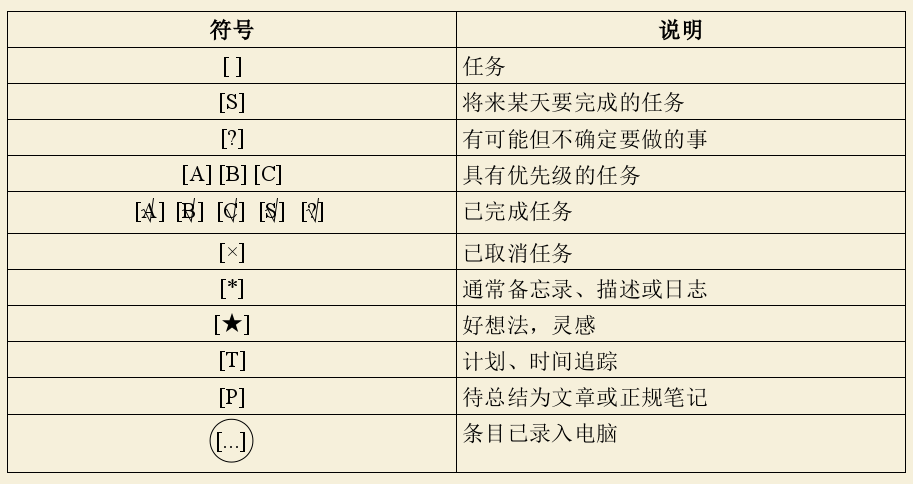
3.1.2 层级符号
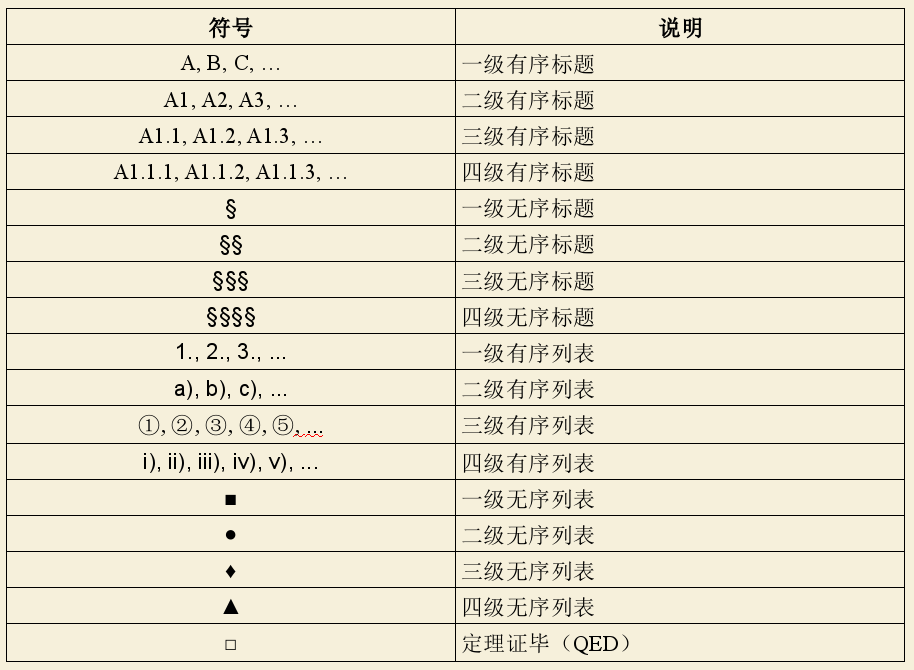
3.1.3 文档关键词声明与交叉引用

3.1.4 数学关键词声明与交叉引用
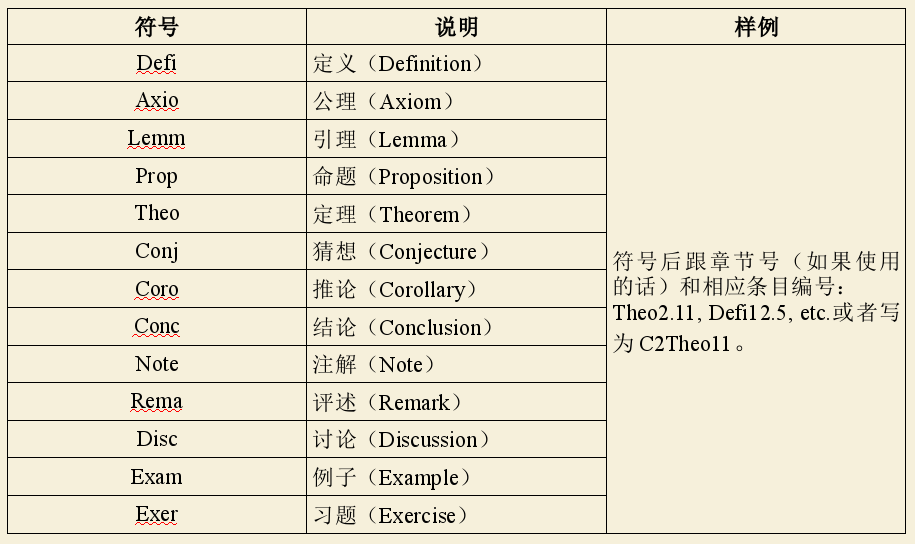
3.1.5 纸质数学笔记颜色
- 正文:铅笔
- 强调:红色
- 评论:黑色
- 分析:蓝色
- 源码或伪代码:粉色
- 文献、公式编号:橙色
- 作图:铅笔或使用打印机套打
3.1.6 iPad数学笔记颜色
- 正文文本:深灰色
- 强调与文本框:红色
- 问题复述与分析,证明或计算过程提纲,思路描述:蓝色
- 备注与评述:绿色
- 源码与伪代码:紫色
- 公式、定理、图片的编号与引用:粉色
- 示意图线条:黑色
3.2 最初想法(05/01/17)
-
数学笔记整理的面临的基本事实
-
大量的数学符号繁多而又抽象
-
即便有Emacs Org mode+cdlatex这样的神器,在电脑上排版也同样非常费时、费力。考虑到记数学笔记的目的并不是为了排出好看的文档,而是为了理解与记忆知识并有效地解决实际问题,将所有的笔记转移到电脑上是得不偿失的。想一想泛函分析课的步尚全老师、Hiptmair教授以及其他的数学系老师,都是用的手写教案,原因便在于此。
-
手写笔记是数学笔记的基本形式。有了手写的草稿后,需要快速整理为规范与美观的笔记时,在GoodNotes中用Apple pencil完成。
-
-
适合用电脑整理的数学笔记
-
数学学习与研究过程中遇到的颇具系统性与美感的结构,如不同的differential form之间的关系,连续函数嵌入链,等等。
-
重要的数学思想与方法
-
自己深有体会的知识点与思想方法
-
有向外传播与展示的需要
-
-
基于文件夹与Emacs Org mode的双重管理
-
将笔记org文件存于math/doc/math-notes文件夹中,其中包括org文档,所需的图片资源,css样式等。
-
一开始不同数学学科分支的笔记可以放到一起,用层次列表来管理。随着以后内容的逐渐增多,可以将不同的分支分类存到不同的文件中。Org mode的树形结构管理起来是很容易的,所以该操作也会很方便。
-
为了能够将笔记完整地导出成网页文件,需要把笔记与数学任务管理分开。否则,即便是给相关的条目加上标签,能够看到目录列表,但也不方便导出。
-
3.3 基本想法(10/08/17)
自己以前主要是用抄书的方式写数学笔记。虽然做得非常详细和工整,但是基本上写完后就没有下文了:既没有复习,也没有修正更新,甚至都没有基本的分类整理、扫描归档,以至于至今还有好多本笔记束之高阁。之所以没有再复习,可能的原因是自己觉得复习这样的笔记是很麻烦的事,已经近乎看原书了。稍微有一点懒惰或者情绪不佳,便不会去做这样的工作。另一方面,这种所谓的“笔记”虽然还比较工整,因其不够规范,更没有用自己的语言和逻辑推导将其严密地串起来,它们还远不能算作正式讲稿、文档或者用于博客。可是,它们又比普通的草稿还好一些,自己便不忍舍弃。如此一来,这些“笔记”也就成了鸡肋,在初学之后就再也没有发挥任何价值。
一个可能更好的方法是:让心境更为宁静、平和,写出相对更为讲究、工整的笔记。但与此同时,又不对其有充当正式文稿的期待。准确地说,就相当于是记录数学日志。这样一来,就可以把自己的学习、思考和推导过程如实记录下来,同时也不会抱以侥幸心理,对它们抱有过多的期待,以至于不去总结更为规范和工整的笔记。
通过以上的分析也可以看出,数学笔记的记录、整理,乃至成为能够公开发表的博客、文章,绝不是一蹴而就的。
在有了上述数学日志后,需将其扫描为PDF文档,在平板电脑上(可以使用GoodNotes)
-
做批注和推导。
-
将错误的部分剪掉。
-
重新组织各块内容,相当于做成剪贴簿。
-
制定一系列的标记符号用于标记:
- 新的重要知识,需整理到正式文档或幻灯片中。
- 重要推导过程,需整理到正式文档或幻灯片中,也可以作为博客文章发布。
- 需要牢记的重要、常用结论,需规整到pocket book中,时时拿出来查看。
- 普通的推导过程、复习已掌握知识的相关部分可以忽略。
-
可以使用计算机帮助推导:Maxima。
基于目前软件功能的现状,数学理论推导与笔记整理的方式制定如下:
-
数学理论推导
-
草稿演算与推导
a) 注意:在数学的初学阶段不要纠结于笔记的工整与否。最好是直接在草稿纸上演算、推导——当然,也要注意平心静气,保持笔迹的工整。将问题都想明白和推导清楚后,再誊写到正式的笔记本上或者录入到电脑上。
b) 上述誊写到正式的笔记本上目前可以变成在GoodNotes用Apple pencil书写。
-
将计算机作为“增智”工具配合草稿纸上的演算与推导
a) 用wxMaxima进行公式符号推导、绘图示意与形象化。
b) 用GNU/Octave进行数值计算、绘图示意与形象化。
c) 对结果进行观察、分析、验证。
d) 注意:重点不在于代码是否工整或优化,而在与迅速把理论算法搞出来,并进行可靠的验证。
-
-
数学笔记整理
-
正式笔记整理与记录
a) 誊写和整理:将草稿上的推导过程与结果、示意图等细心誊写和整理到正式的笔记本上。这就相当于老师的教案了。
b) 扫描归档:用专业扫描仪批量完成笔记的扫描工作,然后在电脑上分类归档,并与推导过程中的计算机程序和计算结果相链接。
c) 注意:不要教条地将任何数学公式都转换为严格的符号系统在wxMaxima里做,或者是在LaTeX里进行排版。传统的纸笔效率其实是很高的。尤其是在画草图、证明定理、涂鸦打草稿、产生新想法等方面,电脑工具是无法与之相比的。所以,绝对不能抛弃,还应进一步加强。
-
用纸笔推导完毕后,要点、重要技术、思想方法等整理录入到LaTeX中。如果已经扫描归档的话,这也不是必需的。
-
将wxMaxima推导得到的数学公式导出为HTML。
-
将LaTeX中的主要思想内容发布为博客。
-
-
数学算法开发与验证
-
用wxMaxima开发出符号计算工具包,可以用于对数值算法进行验证和测试。
-
在Octave中进行数值算法的验证:忒修斯之船方法
a) 将已有的Octave与C++之间数据结构的转换做成通用的库或者头文件。
b) 良好设计之后,用C++实现生产代码。
-
3.4 基于Maxima的数学笔记(08/29/17)
完全在wxMaxima中做数学笔记是不现实的,虽然其符号计算功能有很强的吸引力,但是作为编辑工具仍有无法解决的硬伤。恐怕只有到了wxMaxima能够完美支持Markdown的时候,才可以完全切换到wxMaxima中做数学笔记和相关的推导。而这一天究竟何时到来还无从知晓。更何况,也已经有了Texmacs这样的工具能够实现类似功能——当然,Texmacs离实用还有不小的距离,就把它忘掉吧!
wxMaxima相对于现有笔记记录方案的缺陷
-
就所见即所得而言,其缺乏LibreOffice的富文本编辑功能,甚至连基本的文本加粗都做不到。
-
就基于源码编辑的方式而言,没有Emacs+AucTeX快速便捷,编写效率低。
-
从整体来说,wxMaxima就相当于一个强大的符号计算内核外配了一个初级的编辑器。
3.5 纸上和iPad上手写笔记的混合记法(09/03/18)
关于纸上和iPad上手写笔记有几个方面的考虑:
-
书写感受:手写笔记下笔时的触感没有那么Apple Pencil那么硬,因而书写更为自然和高效,思想也更加自由和放松。
-
涂改:手写笔迹修改不够方便:使用钢笔的话会将卷面搞得很脏很乱;而用铅笔的话则会将桌面搞得比较脏。若采用Apple Pencil的话,则可以生成非常干净美观的文稿,也不会把环境搞脏。
-
绘图:在手写笔记中无法画出美观、精确的示意图。而这一点用iPad上的GoodNotes完胜。
-
对视力的影响:在光线条件好的情况,且使用米黄色的道林纸,手写笔记对于视力的影响是很小的,从而可以保证更长的工作时间——当然,每隔二十五分钟的定时休息仍是必要的。相比之下,直接在iPad上对着发光的屏幕写,则容易引起视疲劳。对此,自己目前将屏幕的色温调到了略微发黄的暖色调,以在最大程度上减小其负面影响。
-
归档管理:通过购买统一的文件夹和标签,并使用活页纸,也是可以将手写笔记管理得比较好的,已经完全可以满足要求——当然,占用一定的空间也是没有办法的事情。使用GoodNotes进行笔记本的管理则更加简单、方便,还可以给页面添加标签,并导出不同的格式以供不同的需要。
综合来看,目前手写笔记本与iPad上的GoodNotes都是不可或缺的。我对它们的定位是手写笔记本用于快速生成原型,GoodNotes用于归整正式笔记文稿。然后再结合以电脑上的生产力工具Markdown和LaTeX,将知识输入。具体如下:
-
将手写笔记用于放飞思想和高效的学习、研究。在精神高度集中的情况下进行理论推导和计算。最终形成自己的手稿。虽然有iPad GoodNotes在,这些纸版的手稿仍需要认真归档管理。
-
用iPad上的GoodNotes对手稿予以进一步地完善、润色。通过誉写、重构、重新绘制精美的示意图,对文稿分类并添加页面标签,形成更为严谨、正式、美观的手写稿。这相当于数学老师上课时用的正式的讲义。
-
以GoodNotes文稿为基础,将经过了反复推敲的成型的内容整理成Markdown文档,用于发布博客文章和幻灯片制作。或者以更为严谨的方式整理为LaTeX文档,成为书稿。
3.6 手写数学笔记的改进(09/08/18)
从之前的笔记中可以发现,自己写得很细致固然不错。但是一个颜色、一个字体毫无区别地一大堆放在一起,根本看不出当初的思路与脉落,亦无法触及和直接把握其中的思想方法。 这样的笔记已经俨然和原书文本没有什么区别了。所以,就像是《论语·八佾篇第三 3.25》所说的“ 子谓韶,「尽美矣,又尽善也。」谓武,「尽美矣,未尽善也。」”,自己在这一点上做得并不好。
针对这个现象和问题,想到可以改进的方面如下:
-
在给出具体的证明之前,要写出分析的思路,并以此作为后续证明的总纲,且便于今后回顾与复习。这里的“分析思路”包括:
a) 基本思想、方法;
b) 解题与证明的大致流程、步骤。
-
具体的证明过程与文字表述则根据之前的文章《如何写数学证明》,按结构化文档的模式来组织、撰写。
-
参照《无敌英语语法》的做法,对关键的内容用不同的颜色高亮和标识,制定统一、一致的样式,将其应用于手写笔记、幻灯片、博客文章。对此,规定采用如下几种颜色进行区分:
a) 正文文本:深灰色
b) 强调与文本框:红色
c) 问题复述与分析,证明或计算过程提纲,思路描述:蓝色
d) 备注与评述:绿色
e) 源码与伪代码:紫色
f) 公式、定理、图片的编号与引用:粉色
g) 示意图线条:黑色
-
写完详细的证明、推导、计算过程后,总结经验与得失。
可以料想到,通过以上几条的改进,再来复习和整理幻灯片时就不会那么困难了。如下图所示为GoodNotes中用于撰写不同内容的缩进量、间距、颜色标识。

3.7 数学笔记的层次与架构(05/13/19)
-
手写本上的笔记
-
相当于最初的探索与草稿。想想钱学森的手稿,这些笔记同样需要认真、工整、细致,方便今后的审核。
-
需要编页码,方便后续整理与归档。
-
-
正式的手写笔记整理到GoodNote中。
-
需要进行系统总结的,整理到LaTeX文档中。为此,需要以Emacs+AUCTeX+LaTeX为核心,将这套工具体系不断地打磨、提升。最终做到人与工具的融合。
3.8 记下暂时不懂的问题(05/25/19)
将暂时不理解的内容和题目统一记在每个笔记本的末尾。这样就可以放下心来站在前人的肩膀上以拿来主义的方式和不求甚解的态度继续前行,同时所有的问题也都如实、详细地记录下来,不用担心将这些知识体系中的漏洞遗忘。待将来有时间的时候,便可以逐一将其补上。
3.9 重新审视当前的数学笔记(11/01/21)
- 做得少、想得多,很多设想的具体实践未形成习惯,数学知识未达到内化的程度。
- 需要明确一点,在数学笔记、演算、整理的工具上目前尚未有大统一的软件。为此,不能完全被动地依赖工具,要将个人的努力与工具的功能结合起来。
- 记录与整理数学笔记这件事绝不可能是一劳永逸的,其他大部分的事情与工作也均如此。若持有这样的想法,并幻想着有某种能够帮助将其实现的大统一的软件工具,则是自己的偷懒情绪在作怪。因此,应摒弃这种不切实际的想法,该需要重复的(如誉写,重新整理排版,格式转换)就一定要踏踏实实地将工作做到位。
- 已有了种种关于数学笔记的想法,接下来最关键的就是要多做、多实践。有了充足的文档、数据、信息,才有整理、重构的物质基础。
- Emacs Org mode用于C++代码的快速验证是合适与便利的。对于需要计算机辅助的数学笔记,则在TeXMacs中操作更为合适。
- 算法的推演、测试,需要详细、准确、一丝不苟地记录下条件、参数、结果。这就像是本科时期完成各种实验课程所要求的实验报告那样。这方面的工作与辛苦是绝不能省的。
- 重视内容、思考,不要在意排版。
3.10 数学重点知识、常用技巧的总结与积累(02/02/22)
将重点数学知识、常用技巧与思想、关键推导环节统一整理到一个LaTeX文档中,起到知识库的作用。之所以采用LaTeX文件格式出于如下考虑:
- 数学笔记的快速录入目前只有基于Emacs AUCTeX mode的LaTeX文档排版才能实现。
- 不同数学环境(Environment),如Definition、Theorem、Remark、Comment等,及其交叉引用,只能在LaTeX文档中方便地实现。之前基于Typora的Markdown排版虽然直观快捷,但不易实现这些功能。
- 这个知识库并不是书本内容的简单抄写与罗列,而是自己对于关键知识形成的真正理解与重要推导过程的总结。
4 数学证明与推导
4.1 如何写数学证明(04/30/18)
一般数学教科书或者专著上给出的证明过程是浑然一体的。即便有其内在的层级和结构关系,也并不容易直接看出。再加上证明中鲜有图示与思路的讲解,使得书本上的证明过程至少在形式上非常抽象、难以理解。读者很容易在追踪作者思维的过程中把原本的目标给跟丢了。为了改进这种表述的形式和方式,在笔记中整理个人的证明过程时,需要做到如下几点:
-
证明前先分析问题,讲清楚证明的目标与思路。
一个数学证明像是一阙音乐段落,都有一个动机(motivation)隐藏其中。对于数学来说,这个动机就是我们常常在好奇心的的驱使下所问的:“定理的提出者或发现者是如何想到这个问题的?”、“完成证明的那灵光一现是如何产生的?”、“换做我自己又该怎样思考”,等等。没有对这个动机的把握,就像是没有灵魂的音乐演奏一般,数学证明也就变成了枯燥、机械的逻辑过程。虽然将其死记硬背下来能考高分,甚至也能够解决实际问题,但却绝不能说由此就掌握了数学。
-
准备好证明所需的技术、工具。这包括必要的定义、定理等。
这要求我们能够“学而时习”,时时查漏补缺。
-
用结构化思维组织证明的步骤与层次架构。
根据我个人的实践体会,手绘的或者专业软件制作的思维导图是整理思维很好的方法。这对于解构需要复杂证明步骤的大定理非常有用。
-
用结构化文档呈现证明的具体过程。
可以使用层级标题、有序和无序列表,并配合以缩进来格式化文档。这里推荐使用轻量级的Markdown撰写原稿。在使文档格式具有足够表现力的同时,既可以避免LaTeX文档编写的繁琐和抽象,也不至于被办公软件提供的多种复杂功能分心。
-
尽量给出能够体现出证明思路的流程图,关键知识点与主要结论的示意图。
在这一点上,James Munkres的拓扑学一书就是很好的典范。同时,日本人在不同专业领域出版的一系列“图解”书籍也很值得借鉴。
-
给出例子,由抽象层次落实到现实案例和具体问题,从而有助于知识点和思路的巩固。
通过以上几个步骤,相信不仅可以巩固自身的知识并强化推理的能力,由此形成的文字也能够为相关领域的其他学习者带来一定的启发,因而是由输入型学习转为输出型学习的良好实践。
4.2 “三张纸方法”(05/22/19)
Christopher Heil在《Writing proofs》这篇文章中介绍了数学证明的基本思路与方法,包括:
-
直接证明:根据已知条件,依据逻辑链条形成的次序推理,直至最终得到期望证明的结论。
-
证明原命题的逆否(contrapositive)命题:逆否命题的逻辑真值表与原命题完全相同,所以二者是等价的。
-
反证法:假设结论不成立,以此作为线索导出已知条件的不成立,从而形成矛盾。在这一点上,反证法即为逆否命题证明法。与此同时,也可以从已知条件和假设结论不成立这两个起点同时出发、“相向”推理,在“路途的中间”得出矛盾。
-
两个命题的等价性证明:需要从正反两个方向证明条件的充分性与必要性。
-
【多个命题的等价性证明:一般采用环形证明法。即,由命题1推出命题2,命题2推出命题3,然后以此类推到命题N-1推出命题N,最后由命题N推出命题1。当然,也不一定严格遵循这样的路径,只要能够保证任意两个命题之间的逻辑是打通的即可。】
-
使用数学归纳法证明任意有限多的情况。【注意,数学归纳法不能推至无穷。】
此外,作者还强调了要用流畅的语言将数学证明的步骤、环节、公式、符号贯穿起来,而不能仅仅是抽象公式、符号的堆砌。【这一点非常重要,数学推导如同编程,需要用连贯的、人能读懂的语言来表达精妙的思想,呈现严谨的逻辑,而绝不只是充满晦涩难懂的怪异符号。】
对于数学证明的过程,作者建议采用“三张纸”方法:
-
第一张纸是草稿,用于在没有任何排版、卷面、格式的约束下抒写想法、自由涂鸦、任意尝试。
-
第二张纸是基于初步形成的思想,尝试性地写出证明。由此得到的材料仍是不完整的、有缺陷的,甚至是错误的。
-
第三张纸是最终的正式稿,要用清晰、流畅的语言完整、干净地写在纸上或者在电脑上排版。
作者在此强调,只有第三张纸的内容出现于教科书、专著和提交的作业。所以,在完美与严谨证明的背后,隐藏了不知多少零乱的涂改、失败的尝试以及学生、学者们的心血。【因此,当我们在苦苦思索后仍寻不到答案时,不要气馁。当同时面对自己零乱的草稿和精美的教科书时,亦不要自惭形秽。数学证明是一个试探的过程,靠的是精雕细琢、不断打磨,而不是一蹴而就。臻于至善也绝不是一日之功!】
Backlinks: 《手写正式笔记的目的》