一曝十寒的人终究一事无成
2020年12月5日我终于将基于四边形单元、用于Galerkin-BEM的Sauter数值奇异积分C++算法调试成功。以(Erichsen and Sauter 1998)文章中的例二作为验证模型,取得了与理论完全一致的结果。至此,终于为我曾在2017年底到2018年初做过的一些关于BEM的理论学习、数学推导和基于Octave的初步验证性实现有了一个圆满的交待。
现在回想起来,之所以拖了这么久才将这个问题解决,一方面是由于我没有为学习与研究立下具体且恒定的目标(而并非没有目标)——正所谓小人常立志,君子才立常志。由于要学、要看的内容非常多,以至于总是见异思迁地切换话题。或者遇到一时无法攻克的难点,往往便转到另一个方向上,从而难以一贯地坚持。然而,总是抱着这种试试看的侥幸态度是注定行不通的。从事科学研究与技术开发,势必要迎难而上才有可能获得进展与成功。
另一方面,因为公司工作的技术方向与我个人立志从事的研究领域不同——这也是出于谋求生存的权宜之计——所以一直以来,我在业余时间开展的学习与研究总会不可避免地受公司项目影响。每年的暑期、年底以及春节后的一段时期,公司项目任务相对松缓,所以下班回家后我还有余力搞一些属于自己的研究。但更多的情况下,我是心有余而力不足,难以将二者兼顾起来。最终酿成的恶果便是个人的数学学习、理论研究与算法开发工作被现实分割得断断续续。理论上迟迟没有系统性进展,代码中潜藏的bug也一直没有彻底解决。这样的情况不恰好印证了“一曝十寒”的道理么!
好在今年我得以集中精力、坚持专注于自己的研究工作,最终解决了上述历史遗留问题,从而也终于有了一个真正属于自己的、可以不断完善算法流程、重构设计与实现并持续提升运行性能的代码基础。由此可以看出,一个人在公司工作——即便是涉及的技术方向与个人研究背景一致,也往往由于无法直奔主题去做核心理论与技术,更多的只是在做应用层面的事情,所以——就像是将自身嫁接到已有的花木上,最终的繁花似锦尽管热闹,但那热闹终究不是自己的,所以至多也就值得捧场一笑,而难获由衷的快慰。而只有立足于个人学习与研究方向而做的基础开发工作,才能够真正为我们扎下根基,并由此萌芽、开花、结果。
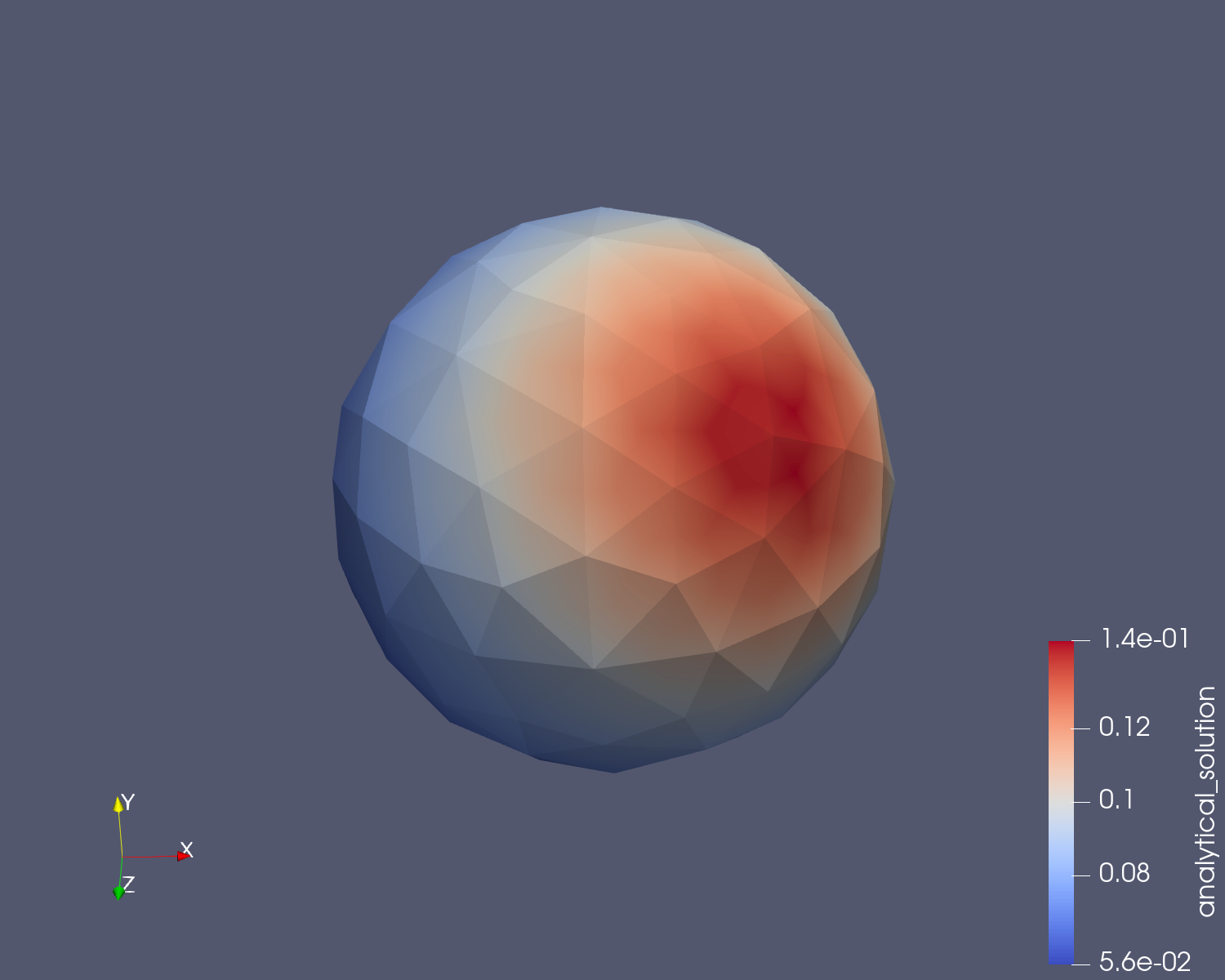

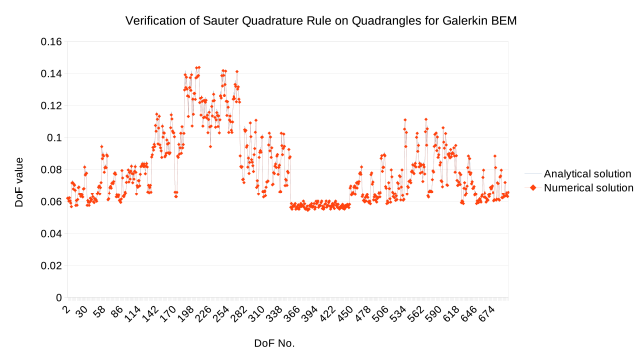
Erichsen, Stefan, and Stefan A. Sauter. 1998. “Efficient Automatic Quadrature in 3-d Galerkin BEM.” Computer Methods in Applied Mechanics and Engineering, Papers presented at the Seventh Conference on Numerical Methods and Computational Mechanics in Science and Engineering, 157 (3): 215–24. https://doi.org/10.1016/S0045-7825(97)00236-3.