In Galerkin BEM, an $\mathcal{H}$-matrix is built with respect to the test and trial spaces of a bilinear form. This bilinear form is related to a boundary integral operator. The test space of the bilinear form is the dual space of the boundary integral operator’s range space and the trial space is the operator’s domain space. In boundary integral equations (BIEs) derived from an elliptic partial differential equation (PDE) with mixed boundary conditions, there are bilinear forms in the BIEs whose test space and/or trial space are defined on an open subset of $\Gamma$. In deal.II, a DoF (degree of freedom) handler, defined with respect to a finite element and a triangulation, holds all DoFs distributed on the triangulation. Therefore, to build an $\mathcal{H}$-matrix for a bilinear form with function spaces on a subdomain, only a subset of DoFs should be selected from the DoF handler, which can then be used to build a cluster tree, block cluster tree and $\mathcal{H}$-matrix.

Elliptic PDE and its boundary integral equations

An elliptic PDE with mixed boundary conditions is given as

\[\begin{equation} \begin{aligned} Lu &= 0 \; (x\in \Omega), \\ \gamma_0^{\rm int}u &= g_{\mathrm{D}} \; (x\in\Gamma_{\mathrm{D}}), \\ \gamma_1^{\rm int}u &= g_{\mathrm{N}} \; (x\in\Gamma_{\mathrm{N}}), \end{aligned} \end{equation}\]

where $L: X \rightarrow X'$ is a self-adjoint second order elliptic partial differential operator, $X$ is a Hilbert space with an inner product $\langle \cdot,\cdot \rangle_X$, $X'$ is the dual space of $X$, $\Gamma$ is the boundary of $\Omega$ and $\Gamma=\overline{\Gamma}_{\mathrm{D}}\cup\overline{\Gamma}_{\mathrm{N}}$.

The general form of $L$ is

\[\begin{equation} \label{eq:diff-operator-2nd-order} (Lu)(x) := -\sum_{i,j=1}^d \frac{\pdiff}{\pdiff x_j} \left[ a_{ji}(x)\frac{\pdiff u}{\pdiff x_{i}} \right] + a_0(x)u(x), \end{equation}\]

where $d$ is the spatial dimension and $a_{ji}(x)=a_{ij}(x)$.

$u\in H^1(\Omega)$ is the potential distribution in $\Omega$. $\gamma_0^{\mathrm{int}} u$ is its interior Dirichlet trace:

\[\begin{equation} \label{eq:interior-dirichlet-trace} (\gamma_0^{\mathrm{int}}u)(x) := \lim_{\Omega\ni\tilde{x} \rightarrow x\in\Gamma} u(\tilde{x}). \end{equation}\]

$\gamma_1^{\mathrm{int}} u$ is the interior co-normal trace or Neumann trace:

\[\begin{equation} \label{eq:interior-conormal-trace} \gamma_1^{\rm int}u(x):=\lim_{\Omega\ni \tilde{x} \rightarrow x \in\Gamma} \left[ \sum_{i,j=1}^d n_j(x)a_{ji}(\tilde{x})\frac{\pdiff u(\tilde{x})}{\pdiff \tilde{x}_i} \right], \end{equation}\]

where $n_j(x)$ is the $j$-th coordinate of the outward unit normal vector $\boldsymbol{n}$ at $x$ on $\Gamma$. The given Dirichlet boundary condition is $g_{\mathrm{D}}\in H^{1/2}(\Gamma_{\mathrm{D}})$ and the Neumann boundary condition is $g_{\mathrm{N}}\in H^{-1/2}(\Gamma_{\mathrm{N}})$.

Testing the PDE $Lu=0$ with an arbitrary $v\in X$ and apply integration by parts, we obtain the Green’s first identity

\[\begin{equation} \label{eq:green-1st-identity-general} a(u,v) = \int_{\Omega} (Lu)(x)v(x) \intd x + \int_{\Gamma} \gamma_1^{\rm int}u(x) \gamma_0^{\rm int}v(x) \intd s, \end{equation}\]

where $a(u,v)$ is a bilinear form

\[\begin{equation} \label{eq:bilinear-form-2nd-order-pde} a(u,v):=\sum_{i,j=1}^d\int_{\Omega}a_{ji}(x)\frac{\pdiff u}{\pdiff x_{i}}\frac{\pdiff v}{\pdiff x_{j}}\intd x + \int_{\Omega}a_0uv \intd x. \end{equation}\]

Because $L$ is self-adjoint, the bilinear form is symmetric, i.e. $a(u,v)=a(v,u)$ and we can obtain the second Green’s identity

\[\begin{equation} \label{eq:green-2nd-identity-general} \int_{\Omega} (Lu)(x)v(x) \intd x - \int_{\Omega}(Lv)(x)u(x) \intd x = \int_{\Gamma}\gamma_1^{\rm int}v(x)\gamma_0^{\rm int}u(x) \intd s - \int_{\Gamma} \gamma_1^{\rm int}u(x)\gamma_0^{\rm int}v(x) \intd s. \end{equation}\]

By replacing the test function $v$ with the fundamental solution $U^{\ast}(x,y)$ of $L$, a representation formula of the potential $u$ as the solution of the homogeneous PDE $Lu=0$ is derived

\[\begin{equation} \label{eq:representation-formula} u(x) = \int_{\Gamma} U^{\ast}(x,y) \gamma_{1,y}^{\mathrm{int}} u(y) \intd s_y - \int_{\Gamma} \gamma_{1,y}^{\mathrm{int}} U^{\ast}(x,y) \gamma_0^{\mathrm{int}} u(y) \intd s_y \quad x\in\Omega. \end{equation}\]

Let the field point $x$ approach the boundary $\Gamma$ and taking the interior Dirichlet trace and Neumann trace of the representation formula, we obtain two BIEs, which form the Calderón system

\[\begin{equation} \label{eq:calderon-system} \begin{pmatrix} \gamma_0^{\rm int} u \\ \gamma_1^{\rm int} u \end{pmatrix} = \begin{pmatrix} (1-\sigma)I - K & V \\ D & \sigma I + K' \end{pmatrix} \begin{pmatrix} \gamma_0^{\rm int} u \\ \gamma_1^{\rm int} u \end{pmatrix}, \end{equation}\]

where

\[\begin{equation} C = \begin{pmatrix} (1-\sigma)I - K & V \\ D & \sigma I + K' \end{pmatrix} \end{equation}\]

is called the Calderón projection operator. This operator describes how to represent either Dirichlet or Neumann data on the boundary $\Gamma$ using the complete Cauchy data $\left\{ \gamma_0^{\mathrm{int}}u,\gamma_1^{\mathrm{int}}u \right\}$. Organizing terms in the Calderón system, then restricting $x$ in the first equation within $\Gamma_{\mathrm{D}}$ and $x$ in the second equation within $\Gamma_{\mathrm{N}}$, we obtain two BIEs for the elliptic PDE with mixed boundary conditions

\[\begin{equation} \begin{aligned} (V \gamma_1^{\mathrm{int}}u)(x) &= \left[ (\sigma I + K) \gamma_0^{\mathrm{int}}u \right](x) \quad x\in\Gamma_{\mathrm{D}}, \\ (D \gamma_0^{\mathrm{int}}u)(x) &= \left\{ \left[ (1-\sigma)I - K' \right] \gamma_1^{\mathrm{int}}u \right\}(x) \quad x\in\Gamma_{\mathrm{N}}. \end{aligned} \label{eq:bies} \end{equation}\]

Extension of boundary conditions and split of boundary traces

The original boundary conditions $g_{\mathrm{D}}$ and $g_{\mathrm{N}}$ are defined on subdomains $\Gamma_{\mathrm{D}}$ and $\Gamma_{\mathrm{N}}$ respectively. We now extend them to the whole boundary as $\tilde{g}_{\mathrm{D}}$ and $\tilde{g}_{\mathrm{N}}$ such that

\[\begin{equation} \begin{aligned} \tilde{g}_{\mathrm{D}}\in H^{1/2}(\Gamma), \tilde{g}_{\mathrm{D}}(x) &= g_{\mathrm{D}}(x) \quad (x\in\Gamma_{\mathrm{D}}), \\ \tilde{g}_{\mathrm{N}}\in H^{-1/2}(\Gamma), \tilde{g}_{\mathrm{N}}(x) &= g_{\mathrm{N}}(x) \quad (x\in\Gamma_{\mathrm{N}}). \end{aligned} \end{equation}\]

Then the Dirichlet trace $\gamma_0^{\mathrm{int}}u$ and Neumann trace $\gamma_1^{\mathrm{int}}u$ on $\Gamma$ can be decomposed as

\[\begin{equation} \gamma_0^{\mathrm{int}}u = \tilde{u} + \tilde{g}_{\mathrm{D}}, \gamma_1^{\mathrm{int}}u = \tilde{t} + \tilde{g}_{\mathrm{N}}, \end{equation}\]

where $\tilde{u}\big\vert_{\Gamma_{\mathrm{D}}} = 0$ and $\tilde{t}\big\vert_{\Gamma_{\mathrm{N}}} = 0$. This means the support of $\tilde{u}$ is contained in $\Gamma_{\mathrm{N}}$ and the support of $\tilde{t}$ is contained in $\Gamma_{\mathrm{D}}$, hence $\tilde{u}\in \tilde{H}^{1/2}(\Gamma_{\mathrm{N}})$ and $\tilde{t}\in\tilde{H}^{-1/2}(\Gamma_{\mathrm{D}})$. Substitute the above decomposition of $\gamma_0^{\mathrm{int}}u$ and $\gamma_1^{\mathrm{int}}u$ into the BIEs in Equation \eqref{eq:bies}, we have

\[\begin{equation} \begin{aligned} V (\tilde{t}+\tilde{g}_{\mathrm{N}})(x) &= (\sigma I + K) (\tilde{u}+\tilde{g}_{\mathrm{D}}) (x) \quad x\in\Gamma_{\mathrm{D}}, \\ D (\tilde{u}+\tilde{g}_{\mathrm{D}})(x) &= \left[ (1-\sigma)I - K' \right] (\tilde{t}+\tilde{g}_{\mathrm{N}}) (x) \quad x\in\Gamma_{\mathrm{N}}. \end{aligned} \end{equation}\]

In the first equation, $(\sigma I \tilde{u})(x)=0$ for $x\in\Gamma_{\mathrm{D}}$, because the term $\sigma I$ only appears if the field point $\tilde{x}$ in the double layer potential $(K\tilde{u})(\tilde{x}) = \int_{\Gamma} \gamma_{1,y}^{\mathrm{int}}U^{\ast}(x,y)\tilde{u}(y) \intd s_y$ can approach to a source point $y$ on $\Gamma$, when we take the limit $\tilde{x}\in\Omega \rightarrow x\in\Gamma$. $\tilde{u}\in\tilde{H}^{1/2}(\Gamma_{\mathrm{N}})$ only has nonzero part in $\Gamma_{\mathrm{N}}$, so the effective integration domain in $K\tilde{u}$ is $\Gamma_{\mathrm{N}}$ and the field point $x$ is outside $\Gamma_{\mathrm{N}}$. Similarly, in the second equation, $\left[ (1-\sigma)I\tilde{t} \right](x) = 0$ for $x\in\Gamma_{\mathrm{N}}$.

After organizing unknown terms to the left and given boundary conditions to the right, the BIEs become

\[\begin{equation} \begin{aligned} V \tilde{t}(x) - K\tilde{u}(x) &= (\sigma I + K)\tilde{g}_{\mathrm{D}}(x) - V \tilde{g}_{\mathrm{N}}(x) \quad x\in\Gamma_{\mathrm{D}}, \\ K'\tilde{t}(x) + D\tilde{u}(x) &= -D\tilde{g}_{\mathrm{D}}(x) + \left[ (1-\sigma)I-K' \right]\tilde{g}_{\mathrm{N}}(x) \quad x\in\Gamma_{\mathrm{N}}. \end{aligned} \end{equation}\]

They can be written in a matrix form as below

\[\begin{equation} \label{eq:bies-in-matrix-form} \begin{pmatrix} V & -K \\ K' & D \end{pmatrix} \begin{pmatrix} \tilde{t} \\ \tilde{u} \end{pmatrix} = \begin{pmatrix} \sigma I + K & -V \\ -D & (1-\sigma) I - K' \end{pmatrix} \begin{pmatrix} \tilde{g}_{\mathrm{D}} \\ \tilde{g}_{\mathrm{N}} \end{pmatrix}. \end{equation}\]

Variational formulation of the BIEs

Test the first BIE in Equation \eqref{eq:bies-in-matrix-form} with $v\in\tilde{H}^{-1/2}(\Gamma_{\mathrm{D}})$ and the second BIE with $q\in\tilde{H}^{1/2}(\Gamma_{\mathrm{N}})$, we obtain the variational formulation

\[\begin{equation} \begin{aligned} b_V(\tilde{t},v) - b_K(\tilde{u},v) &= b_{\sigma I+K}(\tilde{g}_{\mathrm{D}},v) - b_V(\tilde{g}_{\mathrm{N}},v), \\ b_{K'}(\tilde{t},q) + b_D(\tilde{u},q) &= -b_D(\tilde{g}_{\mathrm{D}},q) + b_{(1-\sigma)I-K'}(\tilde{g}_{\mathrm{N}},q). \end{aligned} \label{eq:variational-form} \end{equation}\]

We can see that all the boundary integral operators $V$, $K$, $K'$ and $D$ as well as their bilinear forms appear two times in the BIEs and the two versions of each operator have different domain spaces. The identity operator $I$ along with its bilinear form also appears two times and they have both different domain spaces and range spaces. Because bilinear forms on different spaces lead to different matrices, we explicitly use subscripts to differentiate them in the BIEs:

\[\begin{equation} \begin{aligned} b_{V_1}(\tilde{t},v) - b_{K_1}(\tilde{u},v) &= b_{\sigma I_1+K_2}(\tilde{g}_{\mathrm{D}},v) - b_{V_2}(\tilde{g}_{\mathrm{N}},v), \\ b_{K_1'}(\tilde{t},q) + b_{D_1}(\tilde{u},q) &= -b_{D_2}(\tilde{g}_{\mathrm{D}},q) + b_{(1-\sigma)I_2-K_2'}(\tilde{g}_{\mathrm{N}},q). \end{aligned} \label{eq:variational-form-with-subscripts} \end{equation}\]

The spaces associated with these operators and bilinear forms are listed below.

\[\begin{equation} \begin{aligned} V_1 &: \tilde{H}^{-1/2}(\Gamma_{\mathrm{D}}) \rightarrow H^{1/2}(\Gamma_{\mathrm{D}}) \quad b_{V_1}: \tilde{H}^{-1/2}(\Gamma_{\mathrm{D}}) \times \tilde{H}^{-1/2}(\Gamma_{\mathrm{D}}) \rightarrow \mathbb{R} \\ K_1 &: \tilde{H}^{1/2}(\Gamma_{\mathrm{N}}) \rightarrow H^{1/2}(\Gamma_{\mathrm{D}}) \quad b_{K_1}: \tilde{H}^{1/2}(\Gamma_{\mathrm{N}}) \times \tilde{H}^{-1/2}(\Gamma_{\mathrm{D}}) \rightarrow \mathbb{R} \\ K_1' &: \tilde{H}^{-1/2}(\Gamma_{\mathrm{D}}) \rightarrow H^{-1/2}(\Gamma_{\mathrm{N}}) \quad b_{K_1'}: \tilde{H}^{-1/2}(\Gamma_{\mathrm{D}}) \times \tilde{H}^{1/2}(\Gamma_{\mathrm{N}}) \rightarrow \mathbb{R} \\ D_1 &: \tilde{H}^{1/2}(\Gamma_{\mathrm{N}}) \rightarrow H^{-1/2}(\Gamma_{\mathrm{N}}) \quad b_{D_1}: \tilde{H}^{1/2}(\Gamma_{\mathrm{N}}) \times \tilde{H}^{1/2}(\Gamma_{\mathrm{N}}) \rightarrow \mathbb{R} \\ I_1 &: H^{1/2}(\Gamma) \rightarrow H^{1/2}(\Gamma_{\mathrm{D}}) \quad b_{I_1}: H^{1/2}(\Gamma) \times \tilde{H}^{-1/2}(\Gamma_{\mathrm{D}}) \rightarrow \mathbb{R} \\ K_2 &: H^{1/2}(\Gamma) \rightarrow H^{1/2}(\Gamma_{\mathrm{D}}) \quad b_{K_2}: H^{1/2}(\Gamma) \times \tilde{H}^{-1/2}(\Gamma_{\mathrm{D}}) \rightarrow \mathbb{R} \\ V_2 &: H^{-1/2}(\Gamma) \rightarrow H^{1/2}(\Gamma_{\mathrm{D}}) \quad b_{V_2}: H^{-1/2}(\Gamma) \times \tilde{H}^{-1/2}(\Gamma_{\mathrm{D}}) \rightarrow \mathbb{R} \\ D_2 &: H^{1/2}(\Gamma) \rightarrow H^{-1/2}(\Gamma_{\mathrm{N}}) \quad b_{D_2}: H^{1/2}(\Gamma) \times \tilde{H}^{1/2}(\Gamma_{\mathrm{N}}) \rightarrow \mathbb{R} \\ I_2 &: H^{-1/2}(\Gamma) \rightarrow H^{-1/2}(\Gamma_{\mathrm{N}}) \quad b_{I_2}: H^{-1/2}(\Gamma) \times \tilde{H}^{1/2}(\Gamma_{\mathrm{N}}) \rightarrow \mathbb{R} \\ K_2' &: H^{-1/2}(\Gamma) \rightarrow H^{-1/2}(\Gamma_{\mathrm{N}}) \quad b_{K_2'}: H^{-1/2}(\Gamma) \times \tilde{H}^{1/2}(\Gamma_{\mathrm{N}}) \rightarrow \mathbb{R} \\ \end{aligned} \end{equation}\]

Discretization of bilinear forms into Galerkin matrices

We use the first order piecewise linear finite element to approximate the Sobolev space $H^{1/2}(\Gamma)$ and write it as $H_h^{1/2}(\Gamma)$. In deal.II, this finite element is an object FE_Q(1). We then use the piecewise constant finite element to approximate the space $H^{-1/2}(\Gamma)$ and write it as $H_h^{-1/2}(\Gamma)$. The corresponding deal.II object is FE_DGQ(0). Two DoF handlers are needed, one for $H_h^{1/2}(\Gamma)$, we call it the DoF handler for the Dirichlet data; one for $H_h^{-1/2}(\Gamma)$, we call it the DoF handler for the Neumann data.

A DoF handler object is created from a finite element and a triangulation. The triangulation is generated for the whole boundary $\Gamma$. Therefore, the DoF handler holds all DoFs distributed on the triangulation. When the function space $H^{1/2}(\Gamma)$ or $H^{-1/2}(\Gamma)$ is restricted to an open subset of $\Gamma$, such as $\Gamma_{\mathrm{D}}$ or $\Gamma_{\mathrm{N}}$, we need to select only part of the DoFs in the DoF handler, which are used to build a cluster tree, block cluster and $\mathcal{H}$-matrix. Next, we will show how to select DoFs for restricted function spaces used by bilinear forms.

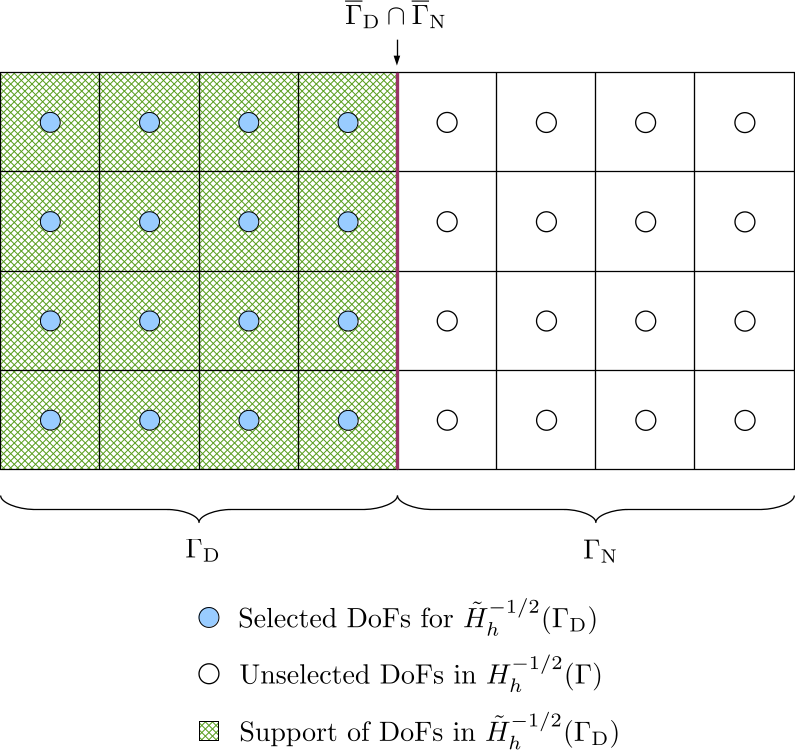
For the finite dimensional space $\tilde{H}_h^{-1/2}(\Gamma_{\mathrm{D}})$ of the unknown Neumann data, we select DoFs in the DoF handler for the Neumann data by iterating over cells with material IDs belonging to the boundary $\Gamma_{\mathrm{D}}$. During the iteration in cells within $\Gamma_{\mathrm{D}}$, the DoF-to-cell topology for the selected DoFs is also built.

The following figure shows the selected DoFs for $\tilde{H}_h^{-1/2}(\Gamma_{\mathrm{D}})$, the unselected DoFs in $H_h^{-1/2}(\Gamma)$, and the support of the DoFs in $\tilde{H}_h^{-1/2}(\Gamma_{\mathrm{D}})$.

$Select DoFs for the finite dimensional space $$\tilde{H}_h^{-1/2}(\Gamma_{\mathrm{D}}) $$ of the unknown Neumann data.$
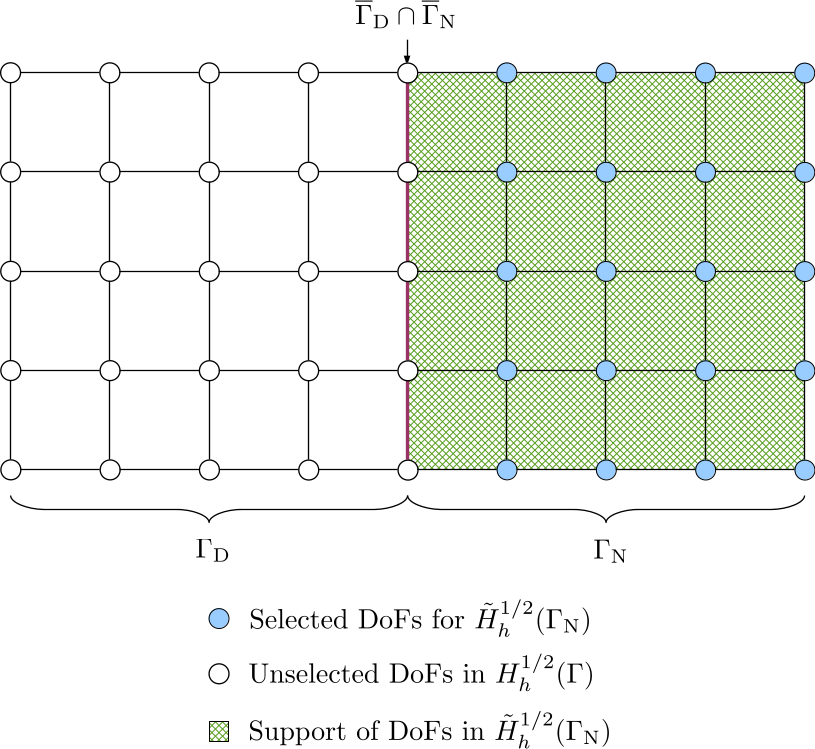
The finite dimensional space $\tilde{H}_h^{1/2}(\Gamma_{\mathrm{N}})$ of the unknown Dirichlet data is a continuous function space and a function in this space vanishes outside $\Gamma_{\mathrm{N}}$. Therefore, the DoFs in $\overline{\Gamma}_{\mathrm{D}}$, i.e. including the interface between $\Gamma_{\mathrm{D}}$ and $\Gamma_{\mathrm{N}}$, should be deselected from $H_h^{1/2}(\Gamma)$. This can be implemented by iterating over cells with material IDs not belonging to $\Gamma_{\mathrm{N}}$ and deselecting their associated DoFs.

The DoF-to-cell topology for the selected DoFs can be built by iterating over cells in $\Gamma_{\mathrm{N}}$.

$Select DoFs for the finite dimensional space $$\tilde{H}_h^{1/2}(\Gamma_{\mathrm{N}}) $$ of the unknown Dirichlet data.$
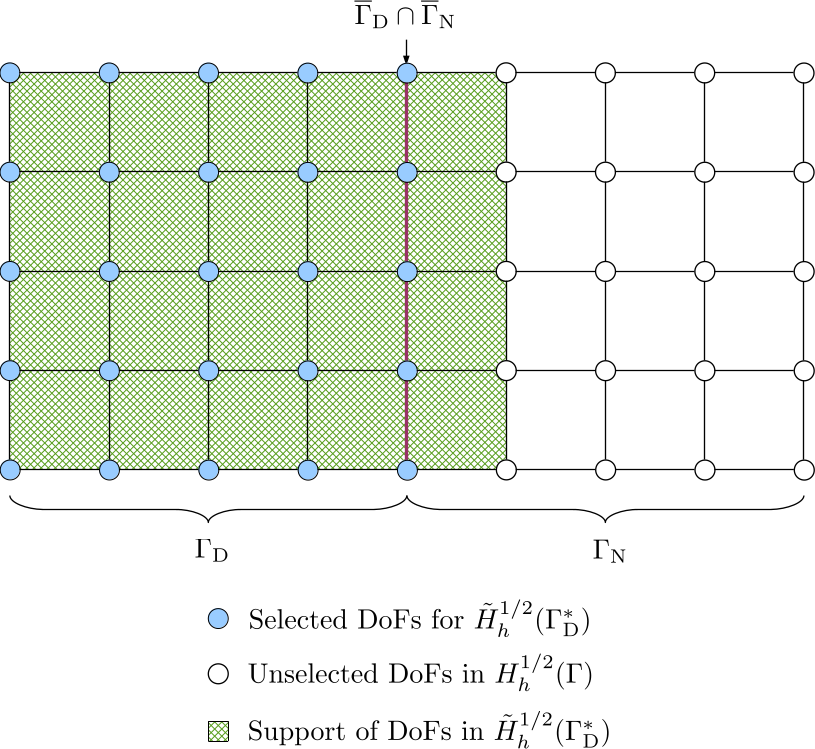
The extended Dirichlet boundary condition $\tilde{g}_{\mathrm{D}}$ belongs to the space $H^{1/2}(\Gamma)$. The extension of $g_{\mathrm{D}}$ from $H^{1/2}(\Gamma_{\mathrm{D}})$ to $H^{1/2}(\Gamma)$ is not unique but should be conforming with $H^{1/2}(\Gamma)$; in particular, the continuity of $\tilde{g}_{\mathrm{D}}$ should be preserved. We can construct $\tilde{g}_{\mathrm{D}}$ by extending $g_{\mathrm{D}}$ with zeros: all DoFs in $\Gamma_{\mathrm{D}}$ are selected from the DoF handler for the Dirichlet data, i.e. from the space $H_h^{1/2}(\Gamma)$, and the support of these DoFs at the interface $\overline{\Gamma}_{\mathrm{D}} \cap \overline{\Gamma}_{\mathrm{N}}$ naturally decays to zero. Consequently, the support of the selected DoFs penetrates one layer of cells into $\Gamma_{\mathrm{N}}$. The resulting discrete space is denoted by $\tilde{H}_h^{1/2}(\Gamma_{\mathrm{D}}^{\ast})$.

Because of support penetration, the DoF-to-cell topology for the selected DoFs should be built by iterating over all cells in the triangulation so that the one layer of cells in $\Gamma_{\mathrm{N}}$ will be included.

$Select DoFs for the finite dimensional space $$\tilde{H}_h^{1/2}(\Gamma_{\mathrm{D}}^{\ast}) $$ of the extended Dirichlet boundary condition.$
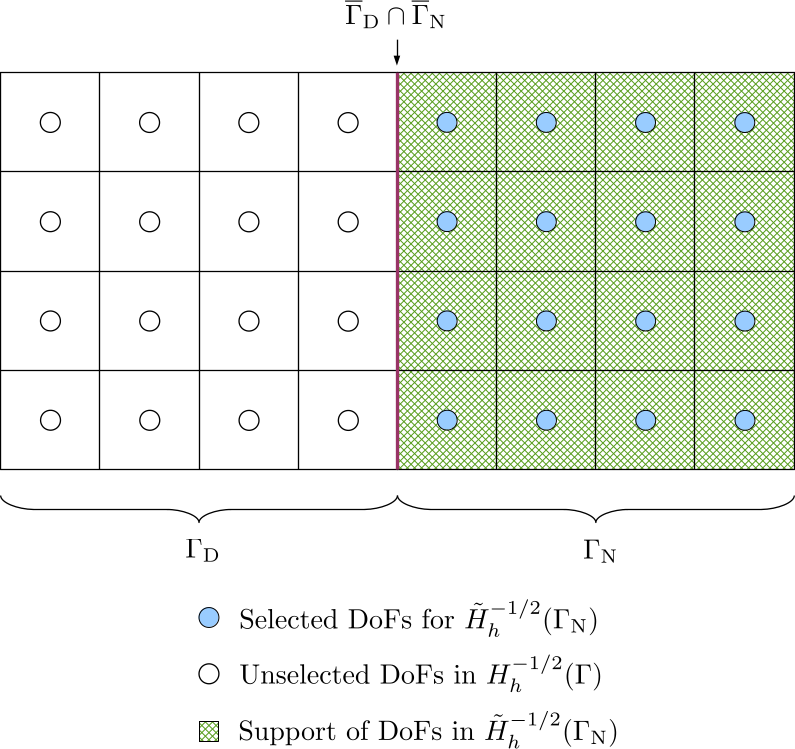
The extended Neumann boundary condition $\tilde{g}_{\mathrm{N}}$ belongs to the space $H^{-1/2}(\Gamma)$. The extension of $g_{\mathrm{N}}$ from $H^{-1/2}(\Gamma_{\mathrm{N}})$ to $H^{-1/2}(\Gamma)$ is also not unique, which should be conforming with $H^{-1/2}(\Gamma)$. Because there is no requirement on function continuity, we can simply extend of $g_{\mathrm{N}}$ with zeros by selecting DoFs in $\Gamma_{\mathrm{N}}$ from the DoF handler for the Neumann data, i.e. from the space $H_h^{-1/2}(\Gamma)$. We denote this function space as $\tilde{H}_h^{-1/2}(\Gamma_{\mathrm{N}})$.

The DoF-to-cell topology for the selected DoFs is built by iterating over cells in $\Gamma_{\mathrm{N}}$.

$Select DoFs for the finite dimension space $$\tilde{H}_h^{-1/2}(\Gamma_{\mathrm{N}}) $$ of the extended Neumann boundary condition.$

After selecting DoFs and building DoF-to-cell topologies for the above four types of spaces, $\mathcal{H}$-matrices can be built on corresponding subdomains for all the bilinear forms in Equation \eqref{eq:variational-form-with-subscripts}. The system of equations in matrix form is

\[\begin{equation} \begin{aligned} \begin{pmatrix} \mathcal{V}_1 & -\mathcal{K}_1 \\ \mathcal{K}_1' & \mathcal{D}_1 \end{pmatrix} \begin{pmatrix} [\tilde{t}] \\ [\tilde{u}] \end{pmatrix} = \begin{pmatrix} \sigma \mathcal{M}_1 + \mathcal{K}_2 & -\mathcal{V}_2 \\ -\mathcal{D}_2 & (1-\sigma) \mathcal{M}_2 - \mathcal{K}_2' \end{pmatrix} \begin{pmatrix} [\tilde{g}_{\mathrm{D}}] \\ [\tilde{g}_{\mathrm{N}}] \end{pmatrix}, \end{aligned} \label{eq:matrix-form} \end{equation}\]

where $\mathcal{K}_1'=\mathcal{K}_1^{\mathrm{T}}$, but $\mathcal{K}_2' \neq \mathcal{K}_2^{\mathrm{T}}$, because they are constructed on different function spaces:

\[\begin{equation} \mathcal{K}_2: \tilde{H}_h^{-1/2}(\Gamma_{\mathrm{D}}) \times \tilde{H}_h^{1/2}(\Gamma_{\mathrm{D}}^{\ast}), \mathcal{K}_2': \tilde{H}_h^{1/2}(\Gamma_{\mathrm{N}}) \times \tilde{H}_h^{-1/2}(\Gamma_{\mathrm{N}}). \end{equation}\]

N.B. When specifying the function spaces for a Galerkin matrix, we place the test space (related to matrix rows) before the trial space (related to matrix columns).

Meanwhile, $\sigma \mathcal{M}_1$ will be directly assembled into $\mathcal{K}_2$ and $(1-\sigma)\mathcal{M}_2$ directly built into $-\mathcal{K}_2'$.