Understanding about the GMRES method
Contents
2 \(AK_m(A,r_0)\) as the test space for measuring the residual vector
3 Construction of orthonormal basis of Krylov subspaces
3.1 Arnoldi’s procedure
3.2 Gram-Schmidt method for orthogonalization
3.3 Householder transformation for orthogonalization
4 Minimization of the residual vector
5 Avoid full matrix/vector multiplications
6 Progressive version of GMRES should be adopted in real applications
7 Summary
Abstract The GMRES method is a kind of Krylov subspace based iterative solver for linear systems. In this article, its key ideas and stages are introduced, which include the selection of search and test spaces, the concept of projection and orthogonal decomposition of the initial residual vector, the motives and essence of the two orthogonalization methods, i.e. Gram-Schmidt and Householder transformation. Finally, the progressive update procedures used in the direct quasi GMRES method are summarized, which is often used in real applications.
GMRES (Generalized minimal residual) is a projection based method for iteratively solving linear systems, where the search space is a Krylov subspace \(\mathcal {K}_m(A,r_0)\) and the test space is \(A \mathcal {K}_m\). The key stages in GMRES is the Arnoldi’s method for construction of an orthonormal basis of the Krylov subspace \(\mathcal {K}_m(A,r_0)\) and the solution of a linear least square problem for minimizing the residual vector norm with the help of Givens transformations.
1 Krylov subspace \(K_m(A,r_0)\) as the search space for the correction vector
For a square \(n\times n\) matrix \(A\), its characteristic polynomial \(\det (\lambda I - A)\) is a monic polynomial in \(\lambda \) of degree \(n\), which can be written as \begin{equation} p_A(\lambda ) = \lambda ^n + c_{n-1} \lambda ^{n-1} + \cdots + c_1 \lambda + c_0. \end{equation} Replace the scalar value \(\lambda \) with the matrix \(A\), we obtain a matrix polynomial \begin{equation} p_A(A) = A^n + c_{n-1}A^{n-1} + \cdots + c_1 A + c_0. \end{equation} The Cayley-Hamilton theorem states that \(p_A(A) = 0\), i.e. the characteristic polynomial \(p_A(A)\) annihilates \(A\). Multiply both sides of \(p_A(A) = 0\) with \(A^{-1}\), we have \begin{equation} A^{n-1} + c_{n-1}A^{n-2} + \cdots + c_1I_n + c_0A^{-1} = 0, \end{equation} which is equivalent to \begin{equation} A^{-1} = -\frac {1}{c_0}A^{n-1} - \frac {c_{n-1}}{c_0} A^{n-2} - \cdots - \frac {c_1}{c_0} I_n. \end{equation} This means \(A^{-1}\) can be represented by a polynomial in \(A\) of degree \(n-1\). If we solve a linear system \(Ax=b\), its solution is \begin{equation} \tilde {x} = A^{-1}b = -\frac {1}{c_0}A^{n-1}b - \frac {c_{n-1}}{c_0} A^{n-2}b - \cdots - \frac {c_1}{c_0} b. \end{equation} Therefore, \(\tilde {x}\) is in the space spanned by \(\left \{ b, Ab, A^2b, \cdots , A^{n-1}b \right \}\), which is just the Krylov subspace \(\mathcal {K}_n(A,b)\).
In an iterative solver like the GMRES method, the solution \(\tilde {x}\) is not directly searched. Instead, we start from an initial guess \(x_0\) and seek a correction vector \(\delta ^{\ast }\) such that \(\tilde {x} = x_0 + \delta ^{\ast }\). This is equivalent to \begin{equation} \begin{aligned} A\tilde {x} &= A(x_0 + \delta ^{\ast }) \\ A\delta ^{\ast } &= r_0 \end{aligned}, \end{equation} where \(r_0=b-Ax_0\) is the initial residual vector. Therefore, the correction vector \(\delta ^{\ast }\) belongs to the Krylov subspace \(\mathcal {K}_n(A,r_0)\).
Definition 1 The grade \(\mu \in \mathbb {N}\) of a vector \(v\) in \(\mathbb {K}^n\) with respect to a matrix \(A\) in \(\mathbb {K}^{n\times n}\) is defined as the minimal degree of the monic polynomial \(p_A(A)\) such that for any \(v\in \mathbb {K}^n\), \(p_A(A)v = 0\).
Obviously, \(\mu \leq n\) according to Cayley-Hamilton theorem. It can also be proved that \(\mu \) is the maximal space dimension that a Krylov subspace \(\mathcal {K}_m(A,v)\) can have for any \(m\in \mathbb {N}\).
For a large linear system, i.e. when \(n\) is large, the true correction vector \(\delta ^{\ast }\) may actually exist in a subspace \(\mathcal {K}_m(A,r_0)\) within \(\mathcal {K}_{\mu }(A,r_0)\). Even though it may exist in a higher dimensional Krylov subspace \(\mathcal {K}_l(A,r_0)\; (l > m)\), we can still use \(\mathcal {K}_m(A,r_0)\) with a small \(m\) to construct its approximation. This is why a Krylov subspace method can be efficient for solving a large scale linear system. The value of \(m\) can either be predefined or progressively increased according to the residual norm of each stage.
2 \(AK_m(A,r_0)\) as the test space for measuring the residual vector
In an iterative solver of a linear system, searching the correction vector \(\delta ^{\ast }\) cannot be finished in just a single step. We can only progressively let \(\delta \) approach to the desired or true correction vector \(\delta ^{\ast }\) until the 2-norm of \(r_0 - A\delta \) is smaller than a predefined threshold.
Let \(r = b - Ax\) be the residual vector. Substitute \(x = x_0 + \delta \) for \(x\), we have \begin{equation} r = b - A(x_0 + \delta ) = b - Ax_0 - A\delta = r_0 - A\delta . \end{equation} So the 2-norm of \(r_0 - A\delta \) is actually the residual norm \(\lVert r \rVert _2\). This is also an orthogonal decomposition of the initial residual vector \(r_0\): \begin{equation} r_0 = A\delta + r, \end{equation} where \(A\delta \) belongs to the space \(A \mathcal {K}_m(A,r_0)\) since \(\delta \in K_m(A,r_0)\). If we select \(A \mathcal {K}_m(A,r_0)\) as the test space for measuring the residual vector \(r\) and we require \(r\) to be orthogonal to \(A \mathcal {K}_m(A,r_0)\), i.e. \(r\in A \mathcal {K}_m(A,r_0)^{\perp }\), then the above expression is an orthogonal decomposition of \(r_0\). This can be illustrated as below.

3 Construction of orthonormal basis of Krylov subspaces
3.1 Arnoldi’s procedure
The Krylov subspace \(K_m(A,r_0)\) is where we want to search the correction vector \(\delta \). Therefore, we need a basis of \(K_m(A,r_0)\) to represent \(\delta \). We already know that \(K_m(A,r_0)\) is spanned by the vectors \(\left \{r_0,Ar_0,A^2r_0,\cdots ,A^{m-1}r_0 \right \}\). However, this is not an orthonormal vector set. Arnoldi’s procedure is used to construct an orthonormal basis based on this vector set, where either the standard Gram-Schmidt method or the Householder transformation can be used for the orthogonalization.
Arnoldi’s procedure is an incremental orthogonalization approach, i.e. we do not explicitly have all the vectors \(\left \{ r_0, Ar_0, \cdots , A^{m-1}r_0 \right \}\) before the algorithm starts, since we should avoid repeated matrix/vector multiplications. Instead, we start from \(r_0\) and normalize it as \(v_1\), then compute \(Av_1\) and construct the second normalized vector \(v_2\) which is orthogonal to \(v_1\), and so on. In general, to construct the \(i\)-th vector \(v_i\) which is orthogonal to all previously computed orthonormal vectors \(v_1,\cdots ,v_{i-1}\), we deal with \(Av_{i-1}\) instead of \(A^i r_0\) in the original set of vectors spanning \(\mathcal {K}_m(A,r_0)\). Because \(v_i\) is orthogonal to all previous vectors \(v_1,\cdots ,v_{i-1}\), this is called full orthogonalization. If we only enforce \(v_i\) to be orthogonal to previous \(k-1\) vectors, i.e. \(\left \{ v_{\max \{1,i-k+1\}},\cdots ,v_{i-1} \right \}\), this is called \(k\)-incomplete orthogonalization. Even though the set of basis vectors \(\left \{ v_1,\cdots ,v_m \right \}\) obtained in this way is different from \(\left \{ r_0,Ar_0,\cdots ,A^{m-1}r_0 \right \}\), it can be proved in Proposition 6.4 on page 160 in (Saad) that both vector sets span the same Krylov subspace \(\mathcal {K}_m(A,r_0)\).
3.2 Gram-Schmidt method for orthogonalization
The Gram-Schmidt method is simply an orthogonal decomposition of a vector, like what we have studied in high school physics. It is illustrated below.

Using the Gram-Schmidt method in the Arnoldi’s procedure, we have \(v_1 = \frac {v}{\lVert v \rVert _2}\). Then the second basis vector before normalization is \begin{equation} w_1 = A v_1 - h_{11} v_1, \end{equation} where \(h_{11} = ( Av_1,v_1 )\). Then the second normalized basis vector is \(v_2 = \frac {w_1}{h_{21}}\) with \(h_{21} = \norm {w_1}_2\). Generally, \begin{equation} v_j = \frac {w_j}{h_{j+1,j}}, \end{equation} where \begin{equation} w_j = Av_j - \sum _{i=1}^j h_{ij}v_i. \end{equation} Or we can write it as \begin{equation} \label {eq:gram-schmidt-recurrence} Av_j = \sum _{i=1}^j h_{ij}v_i + h_{j+1,j} v_j = \sum _{i=1}^{j+1} h_{ij} v_i. \end{equation}
This recurrence relation makes the Gram-Schmidt method numerically unstable due to the following factors.
-
Two large floating numbers may involve in the subtraction in the above equation, which produces a very small value, hence it leads to large numerical errors.
-
Mutiple terms are subtracted from \(Av_j\) and the order of performing these subtractions influences the result.
-
In a normal Gram-Schmidt procedure instead of the specific Arnoldi’s procedure discussed here, if the order of the given set of vectors changes, the results may deviate from the true values because the order of subtractions matters.
If we place all the orthonormal \(v_i\)’s as column vectors into a matrix \(V_m = [v_1,\cdots ,v_m]\) and also place those \(h_{ij}\) coefficients into a matrix \(\overline {H}_m\), according to Equation 12, we have \begin{equation} \label {eq:gram-schmidt-matrix-relation} AV_m = V_{m+1} \overline {H}_m. \end{equation} If we examine the \(j\)-column of Equation 13, the right hand side only involves non-zero coefficients \(h_{ij}\) with \(i=1,\cdots ,j+1\). Therefore, \(\overline {H}_m\) is a Hessenberg matrix, whose matrix pattern or band structure is governed by the above recurrence relation.
3.3 Householder transformation for orthogonalization
The essence of Householder transformation is reflection about a hyperplane. This hyperplane bisects the angle between the input and output vectors of the Householder transformation. This is illustrated in the following figure.

In a Householder transformation which is used for orthogonalization, the output vector is chosen to be in the direction of \(\boldsymbol {e}_1\), i.e. the first basis vector of the Cartesian space. Because the input vector is only rotated and its norm is preserved, a Householder transformation is unitary.
In the Arnoldi’s procedure, a series of Householder transformations \(\left \{ P_i \right \}_{i=1}^m\) are applied consecutively to the set of vectors \(\left \{ r_0,Av_1,Av_2,\cdots ,Av_m \right \}\) to be orthogonalized (N.B. It has one more vector \(Av_m\) in the set than we actually need for the basis of \(\mathcal {K}_m(A,r_0)\)). In the matrix form, we have this relation \begin{equation} P_mP_{m-1}\cdots P_1 [r_0,Av_1,Av_2,\cdots ,Av_m] = [h_0,h_1,\cdots ,h_m], \end{equation} where \(h_0 = \norm {r_0}_2 \boldsymbol {e}_1\), \(h_i (i=1,\cdots ,m)\) in \(\mathbb {K}^n\) is the \(i\)-th column of \(\overline {H}_m\) (in \(\mathbb {K}^{m+1}\)) appended with \(n-i-1\) zeros. This means \begin{equation} [h_1,\cdots ,h_m] = \begin {pmatrix} \overline {H}_m \\ 0_{(n-m-1)\times m} \end {pmatrix}_{n\times m}. \end{equation} N.B. The effect of \(P_i\) is not a Householder transformation working on a vector in \(\mathbb {K}^n\), but on a smaller vector in \(\mathbb {K}^{n-i+1}\). The matrix block structure of \(P_i\) is \begin{equation} P_i = \begin {pmatrix} I_{i-1} & 0 \\ 0 & \overline {P}_i \end {pmatrix}, \end{equation} where \(I_{i-1}\) is an identity matrix with a size \(i-1\) and \(\overline {P}_i\) is the standard Householder transformation working on a vector in \(\mathbb {K}^{n-i+1}\). Therefore, \(P_i\) only influences the sub-block \([i:n, i:m+1]\) of the matrix \([r_0,Av_1,\cdots ,Av_m]\).
Because \(\overline {H}_m\) is a Hessenberg matrix, by adding one column \(h_0\) before it, \([h_0,h_1,\cdots ,h_m]\) is an upper triangular matrix. Let \(Q_m = P_mP_{m-1}\cdots P_1\), which is a unitary matrix, we have \begin{equation} [r_0,Av_1,\cdots ,Av_m] = Q_m^{\mathrm {T}} [h_0,h_1,\cdots ,h_m], \end{equation} which is just a QR decomposition of the matrix on the left hand side. Because the rows of \([h_0,h_1,\cdots ,h_m]\) from \(m+2\) to \(n\) are all zeros, only the first \(m+1\) columns of \(Q_m^{\mathrm {T}}\) are effective in the multiplication \(Q_m^{\mathrm {T}} [h_0,h_1,\cdots ,h_m]\). We write these \(m+1\) columns as a new matrix \(\tilde {V}_{m+1}\). If we also remove the first column from the above equation, we finally have \begin{equation} [Av_1,\cdots ,Av_m] = AV_m = \tilde {V}_{m+1}\overline {H}_m. \end{equation} Compare this equation with Equation 13, \(\tilde {V}_{m+1}\) should be the same as the previous matrix \(V_{m+1}\), the first \(m\) columns of which comprise the orthonormal basis of the Krylov subspace \(\mathcal {K}_m(A,r_0)\).
From this we can see that the Householder transformation for orthogonalization is actually a QR decomposition. Due to this fact, it is not possible to realize incomplete orthogonalization using the Householder transformation.
4 Minimization of the residual vector
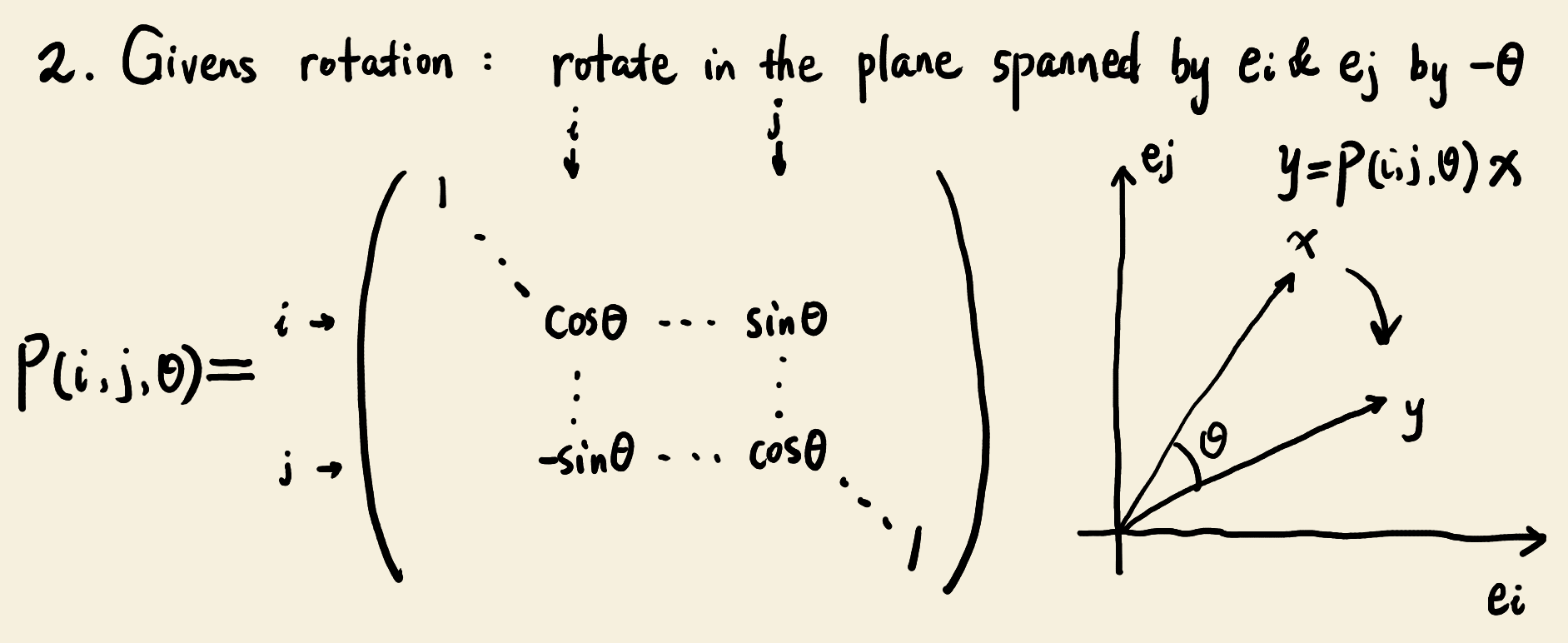
By minimizing the residual vector norm \(\lVert b-Ax \rVert _2 = \lVert \beta \boldsymbol {e}_1 - \overline {H}_m y \rVert _2\), we can obtain the vector \(y\) as the least square solution. \(y\) contains the expansion coefficients of the correction vector \(\delta \) under the basis \(\left \{ v_1,\cdots ,v_m \right \}\). Because \(\overline {H}_m\) is a Hessenberg matrix, using a series of Givens transformations can convert it into an upper triangular matrix, which is then easy to solve.
Givens transformation is a clockwise rotation in the plane spanned by the i-th and j-th basis vectors, which is illustrated below.
5 Avoid full matrix/vector multiplications
A Householder matrix has the form \(P = I - 2 w w^{\mathrm {T}}\), which comprises an self outer product of the normal vector \(w\) of the reflection plane. Hence there is no need to store \(P\) as a full matrix and only saving \(w\) is enough. When \(P\) multiplies a vector \(x\), full matrix/vector multiplication can be avoided. We just compute the inner product of \(w\) and \(x\), then use the resulted scalar value as well as the factor 2 to scale \(w\) and subtract the result vector from \(x\).
Because a Givens transformation \(\Omega _m\) has the structure \begin{equation} \Omega _m = \begin {pmatrix} I_{m-1} & 0 \\ 0 & \begin {pmatrix} c_m & s_m \\ -s_m & c_m \end {pmatrix} \end {pmatrix}, \end{equation} its effective part is the bottom-right \(2\times 2\) block. When \(\Omega _m\) multiplies a vector, only this \(2\times 2\) block takes effect and we only modify the two corresponding entries in the output vector.
6 Progressive version of GMRES should be adopted in real applications
In the implementation of an iterative solver, we desire to save memory by not storing intermediate vectors and making the algorithm progressively update related variables. The direct version of quasi GMRES (DQGMRES) method realizes this concept. Another benefit of the progressive DQGMRES is that we do not have to prescribe the dimension \(m\) of the Krylov subspace \(\mathcal {K}_m(A,r_0)\). Actually, we have no idea about how to select an appropriate \(m\). Instead, \(m\) starts from 1 and gradually increases until the residual vector norm is smaller than a predefined threshold.
In the \(m\)-th iteration of DQGMRES, the following steps should be carried out.
-
Compute the last the column of \(\overline {H}_m^{(m-1)}\), where the superscript \(m-1\) means the original matrix \(\overline {H}_m\) has been applied \(m-1\) times of Givens transformations. If we use Gram-Schmidt \(k\)-incomplete orthogonalization, only these entries \(h_{im}, i=\max \{1,m-k+1\},\cdots ,m+1\) are non-zero.
-
Compute \(w_m = Av_m - \sum _{i=\max \{1,m-k+1\}}^m h_{im}v_i\).
-
Compute \(v_{m+1} = \frac {w_m}{h_{m+1,m}}\).
-
Compute the \(2\times 2\) block in the current Givens transformation matrix \(\Omega _m\).
-
Update \(\overline {g}_m\) and \(g_m\) as below. \begin{equation} \begin{aligned} \overline {g}_m &= \Omega _m \begin {pmatrix} \overline {g}_{m-1} \\ 0 \end {pmatrix} = \begin {pmatrix} I_{m-1} & 0 \\ 0 & \begin {pmatrix} c_m & s_m \\ -s_m & c_m \end {pmatrix} \end {pmatrix} \begin {pmatrix} g_{m-1} \\ \overline {g}_{m-1}[m] \\ 0 \end {pmatrix} \\ &= \begin {pmatrix} g_{m-1} \\ c_m \overline {g}_{m-1}[m] \\ -s_m \overline {g}_{m-1}[m] \end {pmatrix} = \begin {pmatrix} g_{m-1} \\ c_m \gamma _m^{(m-1)} \\ -s_m \gamma _m^{(m-1)} \end {pmatrix} = \begin {pmatrix} g_{m-1} \\ \gamma _m^{(m)} \\ \gamma _{m+1}^{(m)} \end {pmatrix} \end{aligned}, \end{equation} \begin{equation} g_m = \overline {g}_m[1:m] = \begin {pmatrix} g_{m-1} \\ c_m \overline {g}_{m-1}[m] \end {pmatrix} = \begin {pmatrix} g_{m-1} \\ \gamma _m^{(m)} \end {pmatrix}, \end{equation} where \(\gamma _{m+1}^{(m)} := -s_m \gamma _m^{(m-1)}\), when \(m=1\), \(\gamma _1^{(0)} = \beta \); \(\gamma _m^{(m)} := c_m \gamma _m^{(m-1)}\), when \(m=1\), \(\gamma _1^{(1)} = g_1 = \beta c_1\).
-
Apply Givens transformation \(\Omega _m\) to the last column of \(\overline {H}_m^{(m-1)}\) and we obtain \(\overline {R}_m\).
Theoretically, we should have \begin{equation}\begin{aligned} \begin {pmatrix} I_{m-1} & 0 \\ 0 & \begin {pmatrix} c_m & s_m \\ -s_m & c_m \end {pmatrix} \end {pmatrix} \begin {pmatrix} \cdots & 0 \\ \cdots & \vdots \\ \cdots & 0 \\ \cdots & h_{m-k}^{(m-1)} \\ \cdots & h_{m-k+1}^{(m-1)} \\ \cdots & \vdots \\ \cdots & h_{m-1,m}^{(m-1)} \\ \cdots & h_{mm}^{(m-1)} \\ \cdots & h_{m+1,m}^{(m-1)} \end {pmatrix} &= \begin {pmatrix} \cdots & 0 \\ \cdots & \vdots \\ \cdots & 0 \\ \cdots & h_{m-k}^{(m-1)} \\ \cdots & h_{m-k+1}^{(m-1)} \\ \cdots & \vdots \\ \cdots & h_{m-1,m}^{(m-1)} \\ \cdots & c_m h_{mm}^{(m-1)} + s_m h_{m+1,m}^{(m-1)} \\ \cdots & 0 \end {pmatrix} \\ &= \begin {pmatrix} \cdots & 0 \\ \cdots & \vdots \\ \cdots & 0 \\ \cdots & h_{m-k}^{(m)} \\ \cdots & h_{m-k+1}^{(m)} \\ \cdots & \vdots \\ \cdots & h_{m-1,m}^{(m)} \\ \cdots & h_{mm}^{(m)} \\ \cdots & 0 \end {pmatrix}. \end{aligned}\end{equation} In the implementation, we only need to modify the last two entries of the last column of \(\overline {H}_m^{(m-1)}\) as below. \begin{equation} \begin{aligned} h_{mm} &:= c_m h_{mm} + s_m h_{m+1,m} \\ h_{m+1,m} &:= 0 \end{aligned}. \end{equation}
-
The solution vector at the \(m\)-th step is \begin{equation} x_m = x_0 + V_m R_m^{-1} g_m = x_0 + P_m g_m, \end{equation} where \(P_m = V_m R_m^{-1}\). \(R_m\) is \(\overline {R}_m\) removed its last row. \(V_m\) is same as before, \([v_1,\cdots ,v_m]\).
Because \begin{equation} \begin{aligned} P_m R_m &= V_m \\ \left [ P_{m-1}, p_m \right ] R_m &= \left [ V_{m-1}, v_m \right ] \\ \sum _{i=m-k}^{m-1} h_{im}^{(m)} p_i + p_m r_{mm} &= \sum _{i=m-k}^{m-1} h_{im}^{(m)}p_i + p_m h_{mm}^{(m)} = v_m \end{aligned}, \end{equation} the last column \(p_m\) of \(P_m\) can be updated as \begin{equation} p_m = \frac {1}{h_{mm}^{(m)}} \left ( v_m - \sum _{i=m-k}^{m-1} h_{im}^{(m)} p_i \right ). \end{equation}
-
Update the last column \(z_{m+1}\) of the matrix \(Z_{m+1}\). \(Z_{m+1}\) is defined as \(Z_{m+1} := V_{m+1} \Pi _m^{\mathrm {T}} = [z_1, \cdots , z_{m+1}]\), where \(\Pi _m = \Omega _m \Omega _{m-1} \cdots \Omega _1\) is the product of Givens matrices.
When \(m=0\), \(z_1=v_1\) and \(\lVert z_1 \rVert _2 = 1\). For a general \(m\), \begin{equation} z_{m+1} = -s_m z_m + c_m v_{m+1}. \end{equation}
-
Because \(x_m = x_0 + P_m g_m\), we can get its recurrence formulation as below. \begin{equation} x_m = x_0 + [P_{m-1},p_m] \begin {pmatrix} g_{m-1} \\ \gamma _m^{(m)} \end {pmatrix} = x_0 + P_{m-1}g_{m-1} + \gamma _m^{(m)} p_m = x_{m-1} + \gamma _m^{(m)} p_m. \end{equation} Therefore, \(x_m\) is updated based on \(x_{m-1}\).
-
Update the residual vector norm as \(\lvert \gamma _{m+1}^{(m)} \rvert \lVert z_{m+1} \rVert _2\) and determine if the algorithm should stop.
7 Summary
-
The GMRES method is a kind of Krylov subspace method, where the search space is \(\mathcal {K}_{m}(A,r_0)\) and the test space is \(A \mathcal {K}_m(A,r_0)\).
-
The vectors to be orthogonalized for a Krylov subspace \(\mathcal {K}_m(A,r_0)\) are \(\left \{ v, Av_1,\cdots ,Av_{m-1} \right \}\).
-
The Gram-Schmidt orthogonalization is numerically unstable, while the Householder transformation has no such an issue. The Gram-Schmidt orthogonalization can be incomplete, while the Householder transformation cannot. The essence of the Householder transformation based orthogonalization is QR decomposition.
-
Progressive version of GMRES should be implementation in a real application.
References