Conclusions related to special matrix patterns
- A diagonal matrix \(\diag(a_1,\cdots,a_n)\) multiplying a matrix \(A\) from left is equivalent to scaling the rows of \(A\) with the diagonal entries \(a_1,\cdots,a_n\) respectively. A diagonal matrix \(\diag(a_1,\cdots,a_n)\) multiplying a matrix \(A\) from right is equivalent to scaling the columns of \(A\) with the diagonal entries \(a_1,\cdots,a_n\) respectively.
-
Multiply a matrix with \(\boldsymbol{e}_i\), the \(i\)-th orthonormal basis vector, we obtain the \(i\)-th column. Multiply \(\boldsymbol{e}_i^{\mathrm{T}}\), the \(i\)-th orthonormal basis vector as a row vector, with a matrix, we obtain the \(i\)-th row.
We should remember that when multiplying from the left, we transform the rows, when from the right, we transform the columns.
-
If a diagonal sub-block of a matrix \(A\) is an identity matrix \(I_k\), when \(A\) multiplies matrix \(B\), in the product matrix \(C\), its rows corresponding to \(I_k\) are the same as those rows in \(B\).
For example, the Householder matrix
\[\begin{equation} \tilde{H}_5 = \begin{pmatrix} I_4 & 0 \\ 0 & H_5 \end{pmatrix} \end{equation}\]multiplies \(B\) is
\[\begin{equation} \begin{pmatrix} I_4 & 0 \\ 0 & H_5 \end{pmatrix} B = \begin{pmatrix} I_4 & 0 \\ 0 & H_5 \end{pmatrix} \begin{pmatrix} B_1 \\ B_2 \end{pmatrix} = \begin{pmatrix} B_1 \\ H_5B_2 \end{pmatrix} \end{equation}\]The Givens matrix multiplication is
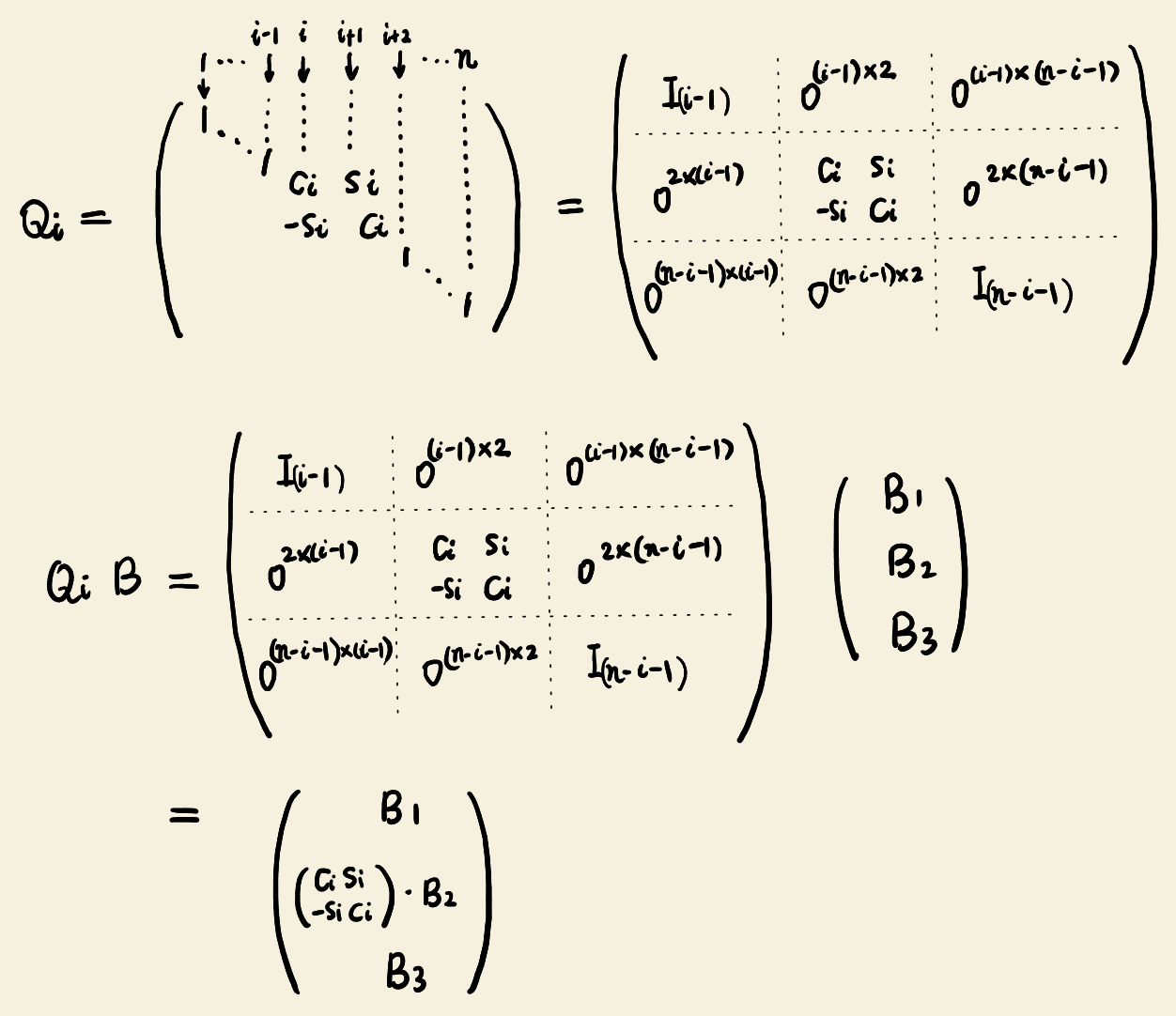
- The product of two upper triangular matrices is an upper triangular matrix. The product of two lower triangular matrices is a lower triangular matrix.
- The product of two diagonal matrices is a diagonal matrices, because a diagonal matrix is both an upper triangular and a lower triangular matrix. The diagonal entries in the result matrix are element-wise product of the diagonal entries in the two operands.
-
The inverse matrix of an upper triangular matrix (if invertible) is an upper triangular matrix.
Solve each column \(v_j\) in \(U^{-1}\) using backward substitution. This is because \(UU^{-1}=I\), which is equivalent to \(U v_j=\boldsymbol{e}_j\). Then we need to prove when \(i > j\), \(v_j[i] = 0\), which is obvious since \(\boldsymbol{e}_j[i]=0\).
Similarly, the inverse matrix of an lower triangular matrix (if invertible) is a lower triangular matrix.
- When there is a zero in the diagonal entries of a triangular matrix, the matrix is not invertible. This is because the determinant of a triangular matrix is equal to the product of its diagonal entries, i.e. all non-diagonal entries do not contribute to the determinant in this case. This can be proved by using cofactor expansion.
-
When a band matrix with \(k_1\) non-zero sub-diagonals in the lower triangular part multiplies with an upper triangular matrix, the band width in the lower triangular part of the result matrix does not change.
When a lower triangular matrix multiplies with a band matrix having \(k_2\) non-zero sub-diagonals in the upper triangular part, the band width in the upper triangular part of the result matrix does not change.
The above conclusions are illustrated in the following figure.

Therefore, when the LU factorization is applied to a band matrix with \(k_1\) non-zero sub-diagonals in the lower triangular part and \(k_2\) in the upper triangular part, the component matrix \(L\) has \(k_1\) non-zero sub-diagonals and \(U\) has \(k_2\) non-zero sub-diagonals.