General theory about the construction of preconditioning bilinear form in BEM
Contents
2 Orthogonal decomposition of the domain \(V^s(\Gamma ,A)\) of \(A\)
3 Define the preconditioning bilinear form
4 Discretization of the preconditioning bilinear form
5 Preconditioners for Laplace problem
In BEM, the preconditioning technique is indispensable for solving a large scale PDE, when an iterative solver, such as CG, GMRES, MinRES, BiCGStab, is adopted. Without a preconditioner, the number of iterations will significantly increase with the deterioration of the system matrix’s condition number. A large condition number can be caused by a large number of DoFs, distinct mesh element size, sharp corners in the geometry, etc.
The procedure for constructing the Galerkin matrix for a preconditioner is summarized into four steps.
-
Find a preconditioning operator having an opposite order with respect to the key operator in the original PDE in the theoretical framework of pseudodifferential operators (see Pseudodifferential operator, Operator preconditioning based on pseudodifferential operator of opposite orders). In BEM, this is a trivial task thanks to the properties of boundary integral operators (see Boundary integral operators considered as pseudodifferential operators).
-
Construct an inverse operator for the preconditioner obtained from the previous step. If the preconditioner is not elliptic on its whole domain, we should construct a Moore-Penrose pseudo inverse or generalized inverse operator instead. Alternatively, we can build an approximate operator for the preconditioner, which is elliptic on the whole domain. Then its inverse operator is available.
-
Construct a bilinear form for the above inverse operator, which is spectrally equivalent to the bilinear form in the variational form of the PDE. The lower bound and upper bound constants in this spectral equivalence condition do not depend on the geometric discretization and finite element (function space) discretization.
-
Discretize the above bilinear form, whose inverse matrix is to be multiplied to the discretized linear system for the variational form of the PDE. Since the inverse operator associated with this bilinear form cannot be directly evaluated, we will compute an approximate version which is based on the inverse matrix of the Galerkin matrix for the preconditioning operator. A general matrix spectral equivalence theorem guarantees the equivalence between this approximate version and the exact version.
In the following, we’ll introduce the basic ideas and theoretical details. Finally, we present the preconditioners used in the Laplace problem with either Dirichlet or Neumann boundary condition.
1 Inverse operator of the preconditioner
The operator \(A: V^s(\Gamma ,A):= H^s(\Gamma )_{/\mathrm {ker}(A)} \rightarrow H^{s-2\alpha }(\Gamma )\) in the original PDE is self-adjoint (in the sense of adjointness in Banach spaces), bounded and \(V^s(\Gamma ,A)\)-elliptic. As a pseudodifferential operator, its order is \(2\alpha \).
The preconditioning operator \(B: H^{s-2\alpha }(\Gamma ) \rightarrow H^s(\Gamma )\) is self-adjoint, bounded and \(V^{s-2\alpha ,0}(\Gamma ,B) := H^{s-2\alpha }(\Gamma )_{/\mathrm {ker}(B)}\)-elliptic. Its order is \(-2\alpha \).
Define the inverse operator \(B^{-1}: H^s(\Gamma ) \rightarrow H^{s-2\alpha }(\Gamma )\) of \(B\) which should be spectrally equivalent to \(A\). Assume \(B\) has a closed range and also note \(B\) is self-adjoint, then \begin{equation} \mathrm {Im}(B) = (\mathrm {ker}(B'))^{\circ } = (\mathrm {ker}(B))^{\circ }. \end{equation} If the operator \(B\) has a non-trivial kernel and let \(H^s(\Gamma )\) be decomposed as \(H^s(\Gamma ) = (\mathrm {ker}(B))^{\circ } \oplus [(\mathrm {ker}(B))^{\circ }]^{\mathrm {c}}\), a generalized inverse \(B^{+}: H^s(\Gamma ) \rightarrow H^{s-2\alpha }(\Gamma )\) can be defined \begin{equation} B^{+} = \begin {cases} \dot {B}^{-1}(y) & y\in (\mathrm {ker}(B))^{\circ } \\ 0 & y\in [(\mathrm {ker}(B))^{\circ }]^{\mathrm {c}} \end {cases}, \end{equation} where \((\mathrm {ker}(B))^{\mathrm {c}}\) is the complement of \(\mathrm {ker}(B)\) within \(H^{s-2\alpha }(\Gamma )\) and \(\dot {B}^{-1}: (\mathrm {ker}(B))^{\circ } \rightarrow (\mathrm {ker}(B))^{\mathrm {c}}\) is a bijective map. Even though the above adjointness and generalized inverse are discussed in the context of Banach spaces, the Sobolev space \(H^{s-2\alpha }(\Gamma )\) is actually a Hilbert space. Therefore, the complement subspace \((\mathrm {ker}(B))^{\mathrm {c}}\) is also the orthogonal complement subspace \((\mathrm {ker}(B))^{\perp }\).
The domain and range spaces of \(\dot {B}^{-1}\) are defined as (Steinbach and Wendland) \begin{equation} \begin{aligned} V^{s,0}(\Gamma ,B) &:= (\mathrm {ker}(B))^{\circ } = \left \{ v\in H^s(\Gamma ): \langle v,v_p \rangle _{H^{s-\alpha }(\Gamma )} = 0 \right \} \\ V^{s-2\alpha ,0}(\Gamma ,B) &:= (\mathrm {ker}(B))^{\perp } = \left \{ v\in H^{s-2\alpha }(\Gamma ): \langle v,v_p \rangle _{H^{s-2\alpha }(\Gamma )}=0 \right \} \end{aligned} \quad \forall v_p\in \mathrm {ker}(B). \end{equation}
To simultaneously ensure \(V^s(\Gamma ,A)\)-ellipticity of \(A\) and \(V^{s,0}(\Gamma ,B)\)-ellipticity of \(\dot {B}^{-1}\) which are required by the spectral equivalence condition, the effective domain for \(A\) and \(\dot {B}^{-1}\) should be the intersection \(V^s(\Gamma ,A) \cap V^{s,0}(\Gamma ,B)\).
2 Orthogonal decomposition of the domain \(V^s(\Gamma ,A)\) of \(A\)
\(V^s(\Gamma ,A)\) is a subspace of \(H^s(\Gamma )\). \(H^s(\Gamma )\) is a Hilbert space and has orthogonal decomposition with respect to its subspace \(V^{s,0}(\Gamma ,B)\): \begin{equation} H^s(\Gamma )=V^{s,0}(\Gamma ,B) \oplus [ V^{s,0}(\Gamma ,B) ]^{\perp }. \end{equation} As defined above, \(V^{s,0}(\Gamma ,B)\) is the annihilator of \(\mathrm {ker}(B)\) in the sense of duality pairing, which can be considered as a generalization of the concept of orthogonality (based on inner product) in a Hilbert space. Its orthogonal complement subspace \([ V^{s,0}(\Gamma ,B) ]^{\perp }\) can then be considered as the counterpart of \(\mathrm {ker}(B) \subset H^{s-2\alpha }(\Gamma )\) but in the dual space \(H^s(\Gamma )\).
For any \(u(x)\in V^s(\Gamma ,A)\), it can be uniquely decomposed as \begin{equation} u(x) = u_0(x) + u_1(x), \end{equation} where \(u_0(x)\in V^{s,0}(\Gamma ,B)\) and \(u_1(x)\in [ V^{s,0}(\Gamma ,B) ]^{\perp }\). Obviously, \(u_0(x)\in V^s(\Gamma ,A) \cap V^{s,0}(\Gamma ,B)\). Because \([ V^{s,0}(\Gamma ,B) ]^{\perp }\) is the counterpart of \(\mathrm {ker}(B)\) in \(H^s(\Gamma )\), if we let \(\{ v_p \}_{p=1}^m\) be the orthonormal basis of \(\mathrm {ker}(B)\), \(u_1(x)\) can be constructed by “projecting” \(u(x)\) to the basis \(\{ v_p \}_{p=1}^m\) in the sense of duality pairing as below. \begin{equation} u_1(x)=\sum _{p=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )} (\mathcal {J}^{-2\alpha }v_p)(x). \end{equation} In this representation, \(\langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )}\) is the expansion coefficient and \(\mathcal {J}^{-2\alpha }v_p\) is the basis element for \([ V^{s,0}(\Gamma ,B) ]^{\perp }\) in \(H^s(\Gamma )\), which is the counterpart of the basis element \(v_p\) for \(\mathrm {ker}(B)\) in \(H^{s-2\alpha }(\Gamma )\). \(\mathcal {J}: \mathcal {S}(\mathbb {R}^d) \rightarrow \mathcal {S}(\mathbb {R}^d)\) is the Bessel potential operator on rapidly decreasing functions. \(\mathcal {J}\) with an order \(s\) is defined as (Steinbach, page 32) \begin{equation} \label {eq:bessel-potential-op} \mathcal {J}^su(x) := ( 2\pi )^{-d/2} \int _{\mathbb {R}^d} ( 1+\lvert \xi \rvert ^2 )^{s/2} \hat {u}(\xi ) \mathrm {e}^{\mathrm {i}\langle x,\xi \rangle } \mathrm {d}\xi , \end{equation} where \(\hat {u}(\xi )\) is the Fourier transform of \(u(x)\). Obviously, the effect of \(\mathcal {J}^s\) on \(u(x)\) is modifying its frequency spectrum by multiplying a polynomial about \(\xi \) with an order \(s\). According to the pseudodifferential operator theory, \(\mathcal {J}^s\) is equivalent to a partial differential operator with an order \(s\). If we restrict the domain of \(\mathcal {J}^s\) to a smaller space instead of \(\mathcal {S}(\mathbb {R}^d)\), such as the Sobolev space \(H^t(\Gamma )\), \(\mathcal {J}^s\) maps from \(H^t(\Gamma )\) to \(H^{t-s}(\Gamma )\), which lowers the Sobolev space order by \(s\). In the above representation for \(u_1(x)\), \(\mathcal {J}^{-2\alpha }\) maps from \(H^{s-2\alpha }(\Gamma )\) to \(H^s(\Gamma )\).
According to (McLean, page 75), for any \(s,t\in \mathbb {R}\) and \(u,v\in \mathcal {S}(\mathbb {R}^d)\), Bessel polynomial operators have these properties:
-
\(\mathcal {J}^{s+t} = \mathcal {J}^s \mathcal {J}^t\)
-
\(( \mathcal {J}^s )^{-1} = \mathcal {J}^{-s}\)
-
\(\mathcal {J}^0 = \text {identity operator}\)
-
\(\langle \mathcal {J}^s u, v \rangle =\langle u,\mathcal {J}^s v \rangle \)
\(\langle \cdot ,\cdot \rangle \) can be either considered as an \(L_2\) inner product of two functions in \(\mathcal {S}(\mathbb {R}^d)\) or as applying a tempered distribution in \(\mathcal {S}'(\mathbb {R}^d)\) to a rapidly decreasing function in \(\mathcal {S}(\mathbb {R}^d)\). For example, we can treat \(u\) as a tempered distribution whose kernel function is \(u\). Then \(\mathcal {J}^s\) in \(\langle \mathcal {J}^s u,v \rangle \) is the Bessel potential operator on \(\mathcal {S}'(\mathbb {R}^d)\) and \(\mathcal {J}^s\) in \(\langle u,\mathcal {J}^s v \rangle \) is the Bessel potential operator on \(\mathcal {S}(\mathbb {R})^d\).
The Sobolev space \(H^s(\mathbb {R}^d)\) is defined as (Steinbach, page 73) \begin{equation} H^s(\mathbb {R}^d) := \left \{ v\in \mathcal {S}'(\mathbb {R}^d): \mathcal {J}^sv \in L_2(\mathbb {R}^d) \right \}. \end{equation} The inner product is for any \(u,v\in H^s(\mathbb {R}^d)\), \begin{equation} \langle u,v \rangle _{H^s(\mathbb {R}^d)} := \langle \mathcal {J}^su, \mathcal {J}^sv \rangle _{L_2(\mathbb {R}^d)}. \end{equation} The norm definition is \begin{equation} \lVert u \rVert _{H^s(\mathbb {R}^d)} := \lVert \mathcal {J}^su \rVert _{L_2(\mathbb {R}^d)}. \end{equation}
From the above, we also have \begin{equation} \langle u,v \rangle _{H^s(\mathbb {R}^d)} = \langle \mathcal {J}^su, \mathcal {J}^sv \rangle _{L_2(\mathbb {R}^d)} = \langle \mathcal {J}^s \mathcal {J}^s u,v \rangle = \langle \mathcal {J}^{2s}u,v \rangle . \end{equation}
The above \(\mathcal {J}^{-2\alpha }\) is actually the Riesz map from \(H^{s-2\alpha }(\Gamma )\) to \(H^s(\Gamma )\), which satisfies \begin{equation} \langle \mathcal {J}^{-2\alpha }u,v \rangle _{H^{s-\alpha }(\Gamma )} = \langle u,v \rangle _{H^{s-2\alpha }(\Gamma )} \quad \forall u,v\in H^{s-2\alpha }(\Gamma ). \end{equation} This can be proved by using the properties of \(\mathcal {J}\). The left hand side of the above equation is \begin{equation} \langle \mathcal {J}^{-2\alpha }u,v \rangle _{H^{s-\alpha }(\Gamma )} = \langle \mathcal {J}^{-\alpha }u, \mathcal {J}^{-\alpha }v \rangle _{H^{s-\alpha }(\Gamma )}, \end{equation} where \(\langle \cdot ,\cdot \rangle _{H^{s-\alpha }(\Gamma )}\) on the left hand side is the duality pairing between \(H^s(\Gamma )\) and \(H^{s-2\alpha }(\Gamma )\), while on the right hand side it is the inner product in \(H^{s-\alpha }(\Gamma )\). Because both \(\mathcal {J}^{-\alpha }u\) and \(\mathcal {J}^{-\alpha }v\) belong to \(H^{s-\alpha }(\Gamma )\), according to the norm definition, \begin{equation} \langle \mathcal {J}^{-\alpha }u, \mathcal {J}^{-\alpha }v \rangle = \langle \mathcal {J}^{s-\alpha }\mathcal {J}^{-\alpha }u, \mathcal {J}^{s-\alpha }\mathcal {J}^{-\alpha }v \rangle _{L_2(\Gamma )} = \langle \mathcal {J}^{s-2\alpha }u,\mathcal {J}^{s-2\alpha }v \rangle _{L_2(\Gamma )}. \end{equation} This is just the same as \(\langle u,v \rangle _{H^{s-2\alpha }(\Gamma )}\).
We can also show that \(u_0(x)\) is orthogonal to \(u_1(x)\). \begin{equation} \begin{aligned} \langle u_0,u_1 \rangle _{H^s(\Gamma )} &= \langle u_0, \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )} \mathcal {J}^{-2\alpha }v_p \rangle _{H^s(\Gamma )} \\ &= \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )} \langle u_0,\mathcal {J}^{-2\alpha }v_p \rangle _{H^s(\Gamma )} \\ &= \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )} \langle \mathcal {J}^su_0,\mathcal {J}^s \mathcal {J}^{-2\alpha }v_p \rangle _{L_2(\Gamma )} \\ &= \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )} \langle \mathcal {J}^su_0,\mathcal {J}^{s-2\alpha }v_p \rangle _{L_2(\Gamma )}, \end{aligned} \end{equation} where \begin{equation} \langle \mathcal {J}^su_0,\mathcal {J}^{s-2\alpha }v_p \rangle _{L_2(\Gamma )} = \langle u_0,v_p \rangle _{H^{s-\alpha }(\Gamma )}. \end{equation} Because \(u_0\in V^{s,0}(\Gamma ,B)\), which is the annihilator of \(\mathrm {ker}(B)\), the above expression is zero.
3 Define the preconditioning bilinear form
Now we define the preconditioning bilinear form \(c(u,w)\), which is spectrally equivalent to \(a(u,w)=\langle Au,w \rangle \)
-
Method 1: Directly construct \(c(u,w)\) based on the generalized inverse \(B^{+}\).
Basic idea: use the above orthogonal decomposition and construct the bilinear form \(c(u,u)\), which is spectrally equivalent to \(a(u,u)=\langle Au,u \rangle \).
Use the boundedness of \(a(\cdot ,\cdot )\) or \(A\), for all \(u\in V^s(\Gamma ,A)\) \begin{equation*} \langle Au,u \rangle _{H^{s-\alpha }(\Gamma )} \leq c_2^A \lVert u \rVert _{H^s(\Gamma )}^2 \end{equation*} Substitute the orthogonal decomposition \(u=u_0+u_1\) \begin{equation*} = c_2^A \lVert u_0 + u_1 \rVert _{H^s(\Gamma )}^2 \end{equation*} Because we are dealing with Hilbert space, \begin{equation*} = c_2^A (\langle u_0,u_0 \rangle + \langle u_0,u_1 \rangle + \langle u_1,u_0 \rangle + \langle u_1,u_1 \rangle ) \end{equation*} Because \(u_0\) is orthogonal to \(u_1\), \begin{align*} &= c_2^A (\lVert u_0 \rVert _{H^s(\Gamma )}^2 + \lVert u_1 \rVert _{H^s(\Gamma )}^2) \\ &= c_2^A \left ( \lVert u_0 \rVert _{H^s(\Gamma )}^2 + \left \langle \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )} \mathcal {J}^{-2\alpha }v_p, \sum _{q=1}^m \langle u,v_q \rangle _{H^{s-\alpha }(\Gamma )} \mathcal {J}^{-2\alpha }v_q \right \rangle \right ) \\ &= c_2^A \left ( \lVert u_0 \rVert _{H^s(\Gamma )}^2 + \sum _{p=1}^m\sum _{q=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )} \langle u,v_q \rangle _{H^{s-\alpha }(\Gamma )} \langle \mathcal {J}^{-2\alpha }v_p, \mathcal {J}^{-2\alpha }v_q \rangle _{H^s(\Gamma )} \right ) \\ &= c_2^A \left ( \lVert u_0 \rVert _{H^s(\Gamma )}^2 + \sum _{p=1}^m\sum _{q=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )} \langle u,v_q \rangle _{H^{s-\alpha }(\Gamma )} \langle v_p,v_q \rangle _{H^{s-2\alpha }(\Gamma )} \right ) \end{align*}
Because \(\{ v_p \}_{p=1}^m\) is an orthonormal basis, \begin{equation*} = c_2^A \left ( \lVert u_0 \rVert _{H^s(\Gamma )}^2 + \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )}^2 \right ) \end{equation*} Use the \(V^{s,0}(\Gamma,B)\)-ellipticity of \(\dot {B}^{-1}\) and the reciprocal relationship between its spectrum and that of \(B\), \begin{align*} &\leq c_2^A \left ( c_2^B \langle \dot {B}^{-1}u_0,u_0 \rangle _{H^{s-\alpha }(\Gamma )} + \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )}^2 \right ) \\ &\leq c_2^A \max \{ c_2^B,1 \} \left ( \langle \dot {B}^{-1}u_0,u_0 \rangle _{H^{s-\alpha }(\Gamma )} + \sum _{k=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )}^2 \right ). \end{align*}
If we define the bilinear form \(c(u,w)\) as \begin{equation} \label {eq:bilinear-form-c} \begin{aligned} c(u,w) &:= \langle B^{\dagger }u,w \rangle _{H^{s-\alpha }(\Gamma )} + \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )} \langle w,v_p \rangle _{H^{s-\alpha }(\Gamma )} \\ &= \langle \dot {B}^{-1}u_0,w_0 \rangle _{H^{s-\alpha }(\Gamma )} + \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )} \langle w,v_p \rangle _{H^{s-\alpha }(\Gamma )} \quad \forall u,w\in H^s(\Gamma ) \end{aligned}, \end{equation} it satisfies the upper part of the spectral equivalence condition \begin{equation} \langle Au,u \rangle _{H^{s-\alpha }(\Gamma )} \leq c_2^A \max \{ c_2^{B},1 \} c(u,u). \end{equation}
Then we prove the lower part of the spectral equivalence condition. Use the \(V^s(\Gamma,A)\)-ellipticity of \(A\), for all \(u\in V^s(\Gamma ,A)\) \begin{equation*} \langle Au,u \rangle _{H^{s-\alpha }(\Gamma )} \geq c_1^A \lVert u \rVert _{H^s(\Gamma )}^2 \end{equation*} Substitute the orthogonal decomposition \(u=u_0+u_1\) \begin{align*} &= c_1^A \lVert u_0+u_1 \rVert _{H^s(\Gamma )}^2 \\ &= c_1^A \left ( \lVert u_0 \rVert _{H^s(\Gamma )}^2 + \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )}^2 \right ) \end{align*}
Use the boundedness of \(\dot {B}^{-1}\) and the reciprocal relationship between its spectrum and that of \(B\) \begin{align*} &\geq c_1^A \left ( c_1^B \langle \dot {B}^{-1}u_0,u_0 \rangle _{H^{s-\alpha }(\Gamma )} + \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )}^2 \right ) \\ &\geq c_1^A \min \{ c_1^B, 1 \} \left ( \langle \dot {B}^{-1}u_0,u_0 \rangle _{H^{s-\alpha }(\Gamma )} + \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-\alpha }(\Gamma )}^2 \right ). \end{align*}
Therefore, we have \begin{equation} c_1^A \min \{ c_1^B,1 \} c(u,u) \leq \langle Au,u \rangle _{H^{s-\alpha }(\Gamma )}. \end{equation}
In these two special cases
-
when \(V^s(\Gamma ,A) \subseteq V^{s,0}(\Gamma ,B)\), the orthogonal decomposition of \(u\) degenerates to \(u=u_0\),
-
\(\mathrm {ker}(B) = \{ 0 \}\)
the bilinear form \(c(u,u)\) degenerates to \(\langle \dot {B}^{-1}u,u \rangle \).
-
-
Method 2: Build an approximate operator \(\tilde {B}\) for \(B\), which is elliptic on the whole domain \(H^{s-2\alpha }(\Gamma )\). Then use its inverse to build the bilinear form \(c(u,w) = \langle \tilde {B}^{-1}u,w \rangle _{H^{s-\alpha }(\Gamma )}\).
For any \(u\in H^{s-2\alpha }(\Gamma )\), it also has an orthogonal decomposition in \(V^{s-2\alpha }(\Gamma ,B) \oplus \mathrm {ker}(B)\) as \begin{equation} u = u_0 + u_1 = u_0 + \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-2\alpha }(\Gamma )} v_p(x), \end{equation} where the inner product \(\langle u,v_p \rangle _{H^{s-2\alpha }(\Gamma )}\) is the expansion coefficient for \(u_1\) and \(v_p\) is the corresponding basis element. Then we try to construct \(\tilde {B}\) which is \(H^{s-2\alpha }(\Gamma )\)-elliptic. \begin{align*} \lVert u \rVert _{H^{s-2\alpha }(\Gamma )}^2 &= \lVert u_0 + u_1 \rVert _{H^{s-2\alpha }(\Gamma )}^2 \\ &= \left ( \lVert u_0 \rVert _{H^{s-2\alpha }(\Gamma )}^2 + \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-2\alpha }(\Gamma )}^2 \right ) \end{align*}
Use the \(V^{s-2\alpha}(\Gamma,B)\)-ellipticity of \(B\) \begin{align*} &\leq \left ( \frac {1}{c_1^B} \langle Bu_0, u_0 \rangle _{H^{s-\alpha }(\Gamma )} + \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-2\alpha }(\Gamma )}^2 \right ) \\ &\leq \max \{ \frac {1}{c_1^B},1 \} \left ( \langle Bu_0, u_0 \rangle _{H^{s-\alpha }(\Gamma )} + \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-2\alpha }(\Gamma )}^2 \right ). \end{align*}
It is equivalent to \begin{equation} c_1^{\tilde {B}} \lVert u \rVert _{H^{s-2\alpha }(\Gamma )}^2 \leq \left ( \langle Bu_0, u_0 \rangle _{H^{s-\alpha }(\Gamma )} + \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-2\alpha }(\Gamma )}^2 \right ), \end{equation} where \(c_1^{\tilde {B}} = 1/\max \{ \frac {1}{c_1^B},1 \} = \min \{ c_1^B,1 \}\).
On the other hand, we start from the boundedness of \(B\): \begin{align*} \lVert u \rVert _{H^{s-2\alpha }(\Gamma )}^2 &= \lVert u_0 + u_1 \rVert _{H^{s-2\alpha }(\Gamma )}^2 \\ &= \left ( \lVert u_0 \rVert _{H^{s-2\alpha }(\Gamma )}^2 + \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-2\alpha }(\Gamma )}^2 \right ) \\ &\geq \left ( \frac {1}{c_2^B} \langle Bu_0,u_0 \rangle _{H^{s-\alpha }(\Gamma )} + \sum _{p=1}^m \langle u,v_0 \rangle _{H^{s-2\alpha }(\Gamma )}^2 \right ) \\ &\geq \min \{ \frac {1}{c_2^B},1 \} \left ( \langle Bu_0,u_0 \rangle _{H^{s-\alpha }(\Gamma )} + \sum _{p=1}^m \langle u,v_0 \rangle _{H^{s-2\alpha }(\Gamma )}^2 \right ). \end{align*}
So we have \begin{equation} \left ( \langle Bu_0, u_0 \rangle _{H^{s-\alpha }(\Gamma )} + \sum _{p=1}^m \langle u,v_p \rangle _{H^{s-2\alpha }(\Gamma )}^2 \right ) \leq c_2^{\tilde {B}} \lVert u \rVert _{H^{s-2\alpha }(\Gamma )}^2, \end{equation} where \(c_2^{\tilde {B}} = \max \{ c_2^B,1 \}\).
Therefore, we can define the bilinear form related to \(\tilde {B}\) as \begin{equation} \label {eq:bilinear-form-b} \begin{aligned} \langle \tilde {B}u,w \rangle _{H^{s-\alpha }(\Gamma )} &= \langle Bu,w \rangle _{H^{s-\alpha }(\Gamma )} + \sum _{p=1}^m \langle v,v_p \rangle _{H^{s-2\alpha }(\Gamma )} \langle w,v_p \rangle _{H^{s-2\alpha }(\Gamma )} \\ &= \langle Bu_0,w_0 \rangle _{H^{s-\alpha }(\Gamma )} + \sum _{p=1}^m \langle v,v_p \rangle _{H^{s-2\alpha }(\Gamma )} \langle w,v_p \rangle _{H^{s-2\alpha }(\Gamma )} \quad \forall u,w\in H^{s-2\alpha }(\Gamma ). \end{aligned} \end{equation} It is both bounded and \(H^{s-2\alpha }(\Gamma )\)-elliptic.
The differences between the bilinear forms in Equation (17) and (23) are:
-
In Equation (23), \(u\) and \(w\) are projected to \(v_p\) via inner product, which is a true projection. In Equation (17), \(u\) and \(w\) are in a different space from \(v_p\). They are “projected” to \(v_p\) via duality pairing, which can be considered as a generalization of projection.
-
In Equation (23), the basis used for function expansion is \(\{ v_p \}_{p=1}^m\). In Equation (17), the basis is \(\{ \mathcal {J}v_p \}_{p=1}^m\).
-
4 Discretization of the preconditioning bilinear form
According to (Steinbach and Wendland, section 4), Method 1 in Section 3 requires coordinate transformation between the finite element basis and the orthonormal basis adopted for the orthogonal decomposition \(V_h^s(\Gamma ,A) = V_h^0 \oplus \{ \mathcal {J}v_p \}_{p=1}^m\), which is more complicated than Method 2. Meanwhile, (Steinbach, section 13.2 page 299) only introduces Method 2. So we stick to this method.
Usually, the inverse operator \(\tilde {B}^{-1}\) cannot be directly evaluated or discretized. We need to compute the discretized matrix of \(\tilde {B}\) first, then use its inverse matrix to compute an approximation to the discretized matrix for the inverse operator \(\tilde {B}^{-1}\). This can be visualized in the following diagram.
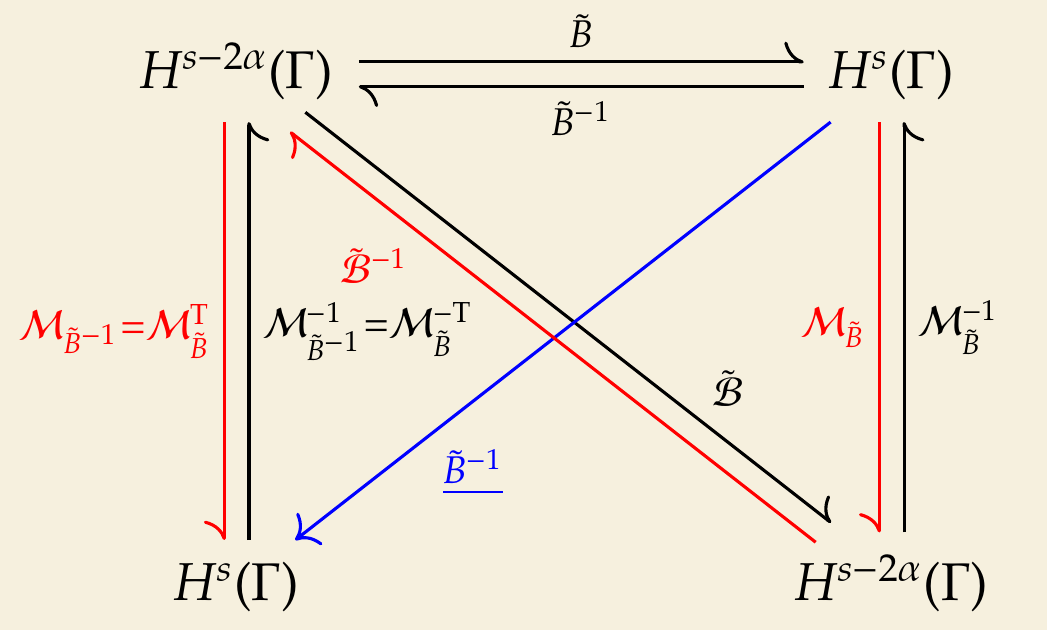
Therefore, we have \begin{equation} \underline {\tilde {B}^{-1}} \approx \mathcal {M}_{\tilde {B}}^{\mathrm {T}} \tilde {\mathcal {B}}^{-1} \mathcal {M}_{\tilde {B}}. \end{equation} The matrix to be multiplied to both sides of the equation is \begin{equation} \mathcal {M}_{\tilde {B}}^{-1} \tilde {\mathcal {B}} \mathcal {M}_{\tilde {B}}^{-\mathrm {T}}. \end{equation}
The spectral equivalence between the above two matrices \(\underline {\tilde {B}^{-1}}\) and \(\mathcal {M}_{\tilde {B}}^{\mathrm {T}} \tilde {\mathcal {B}}^{-1} \mathcal {M}_{\tilde {B}}\) can be proved using the theory given in (Steinbach and Wendland, section 3). This theory is described in a general form as below.
\(V\) and \(W\) are two Hilbert spaces. \(A: V \rightarrow V'\) is a \(V\)-elliptic, self-adjoint and bounded operator, while \(B: W \rightarrow V'\) is any bounded operator. Define an operator \(T: W \rightarrow W'\) as \(T = B' A^{-1} B\). In principle, it has a Galerkin matrix \(\mathcal {T}\). In reality, this matrix cannot be directly computed. The Galerkin matrices for \(A\) and \(B\) are \(\mathcal {A}\) and \(\mathcal {B}\) respectively. Then we have another matrix \begin{equation} \tilde {\mathcal {T}} = \mathcal {B}^{\mathrm {T}} \mathcal {A}^{-1} \mathcal {B}. \end{equation} It can be proved that for any \(w_h\in W_h\), \begin{equation} ( \tilde {\mathcal {T}} \underline {w}, \underline {w} ) \leq ( \mathcal {T} \underline {w}, \underline {w} ). \end{equation} If the stability condition or \(\inf \sup \) condition is satisfied \begin{equation} \inf _{0\neq w_h\in W_h} \sup _{0\neq v_h\in V_h} \frac {\lvert \langle Bw_h,v_h \rangle _{V} \rvert }{\lVert w_h \rVert _W \lVert v_h \rVert _V} \geq c, \end{equation} we also have \begin{equation} \gamma ( \mathcal {T} \underline {w}, \underline {w} ) \leq ( \tilde {\mathcal {T}} \underline {w}, \underline {w} ). \end{equation} Therefore, \(\mathcal {T}\) and \(\tilde {\mathcal {T}}\) are spectrally equivalent.
The relationship between the spaces, operators and matrices are shown below.
Coming back to the spectral equivalence between the two matrices \(\underline {\tilde {B}^{-1}}\) and \(\mathcal {M}_{\tilde {B}}^{\mathrm {T}} \tilde {\mathcal {B}}^{-1} \mathcal {M}_{\tilde {B}}\), we can see that it is the special case when \(W\) is selected to be \(V'\) and \(B\) is the identity operator on \(V'\). The mass matrix \(M_A\) for the duality pairing from \(V'\) to \(V\) is just the Galerkin matrix of \(B\). This is shown in the following figure.
5 Preconditioners for Laplace problem
The operator equation for the Laplace problem with Dirichlet boundary condition is \begin{equation} \langle Vt, \tau \rangle _{\Gamma } = \langle (\frac {1}{2}I + K)g, \tau \rangle _{\Gamma } \quad \forall \tau \in H^{-1/2}(\Gamma ). \end{equation} The hypersingular operator \(D\) has an opposite order with respect to \(V\), which is naturally the preconditioner for this equation. However, according to here, \(D\) is not \(H^{1/2}(\Gamma )\)-elliptic, but only \(H_{\ast }^{1/2}(\Gamma )\)-elliptic or \(H_{\ast \ast }^{1/2}(\Gamma )\)-elliptic depending on which kind of inner product is desired. To avoid the complex of computing the natural density \(w_{\mathrm {eq}}\), we choose \(H_{\ast \ast }^{1/2}(\Gamma )\)-ellipticity. Then the bilinear form associated with the regularized or gauged operator \(\tilde {D}\) is \begin{equation} \langle \tilde {D}u,w \rangle = \langle Du,w \rangle + \langle u,1 \rangle _{\Gamma } \langle w,1 \rangle _{\Gamma } \quad \forall u,w\in H^{1/2}(\Gamma ). \end{equation} Then the inverse of the preconditioning matrix is \begin{equation} \mathcal {M}_{\tilde {D}}^{-1} \tilde {\mathcal {D}} \mathcal {M}_{\tilde {D}}^{-\mathrm {T}}, \end{equation} where \(\mathcal {M}_{\tilde {D}}\) is the mass matrix for the duality pairing from \(H^{-1/2}(\Gamma )\) to \(H^{1/2}(\Gamma )\).
The operator equation for the Laplace problem with Neumann boundary condition is \begin{equation} \langle Du, v \rangle _{\Gamma } + \alpha \langle u,1 \rangle _{\Gamma } \langle v,1 \rangle _{\Gamma } = \langle (\frac {1}{2}I - K')g,v \rangle _{\Gamma } \quad \forall v\in H^{1/2}(\Gamma ). \end{equation} The single layer potential operator \(V\) has an opposite order with respect to \(D\), which is the preconditioner. When \(d=3\), \(V\) is \(H^{-1/2}(\Gamma )\)-elliptic, so we directly obtain the inverse of the preconditioning matrix \begin{equation} \mathcal {M}_V^{-1} \mathcal {V} \mathcal {M}_V^{-\mathrm {T}}, \end{equation} where \(\mathcal {M}_V\) is the mass matrix for the duality pairing from \(H^{1/2}(\Gamma )\) to \(H^{-1/2}(\Gamma )\).
References
William Charles Hector McLean. Strongly Elliptic Systems and Boundary Integral Equations. Cambridge University Press. ISBN 978-0-521-66375-5.
Olaf Steinbach. Numerical Approximation Methods for Elliptic Boundary Value Problems: Finite and Boundary Elements. Springer Science & Business Media. ISBN 978-0-387-31312-2.
Olaf Steinbach and Wolfgang L. Wendland. The construction of some efficient preconditioners in the boundary element method. 9(1-2):191–216. URL http://link.springer.com/article/10.1023/A:1018937506719.