Abstract

  1. The meaning of full column rank and full row rank of a matrix, which are related to the injective and surjective property of the linear map defined by the matrix.
  2. The relationship between the injective or surjective property and the left or right inverse of a matrix.
  3. The relationship between the kernel and range spaces of a matrix and its transpose. In linear operator theory, this corresponds to a linear operator and its adjoint operator.

Let \(A\) be a matrix in \(\mathbb{K}^{m\times n}\) mapping from the vector space \(V^n\) to \(W^m\). \(A^{\ast}\) is its transpose matrix, when \(\mathbb{K}=\mathbb{R}\). When \(\mathbb{K}=\mathbb{C}\), \(A^{\ast}\) is its Hermite transpose matrix, i.e. complex conjugate with transpose. \(A\) can also be a general bounded linear operator mapping from \(V\) to \(W\), where \(V\) and \(W\) are Hilbert spaces. \(A^{\ast}\) is the Hilbert adjoint operator mapping from \(W\) to \(V\). N.B. \(V\) and \(W\) should not be Banach spaces and the Banach adjoint operator \(A'\) maps from \(W^{\ast}\) to \(V^{\ast}\), instead of \(W\) to \(V\).

Then we have the following conclusions:

  • The row space of \(A\) is the column space of \(A^{\ast}\) and the column space of \(A\) is the row space of \(A^{\ast}\).
  • If a linear map is injective, it has a left inverse operator. If it is surjective, it has a right inverse operator.

  • When a matrix \(A\) has full row rank \(r=m\):

    • The column rank of \(A\) is also \(r\) and \(n\geq r\). For any vector \(y\in \mathbb{R}^m=\mathbb{R}^r\), it can be linearly represented by the \(n\) column vectors of \(A\). If \(n=r\), such a representation is unique. If \(n>r\), the \(n\) column vectors of \(A\) are not linearly independent and the representation is not unique. In both cases, the representation is achievable and the linear map defined by \(A\) must be surjective.
    • \(A^{\ast}\) has full column rank and the linear map defined by \(A^{\ast}\) is injective.
    • \(A\) has a right inverse and \(A^{\ast}\) has a left inverse.

    img

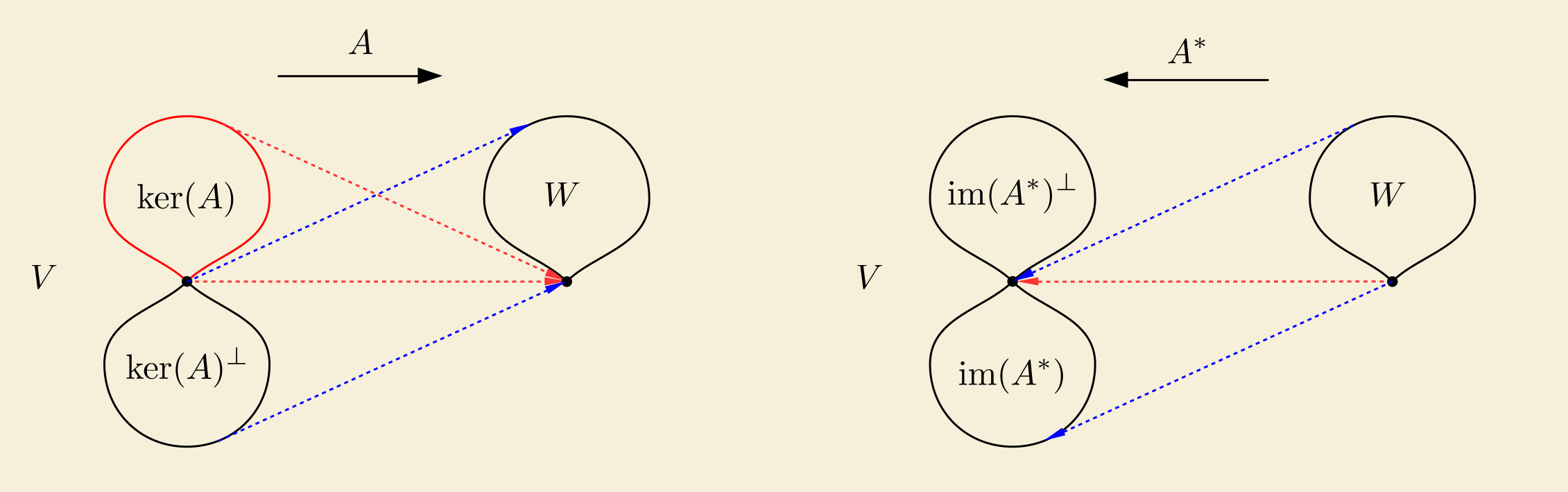
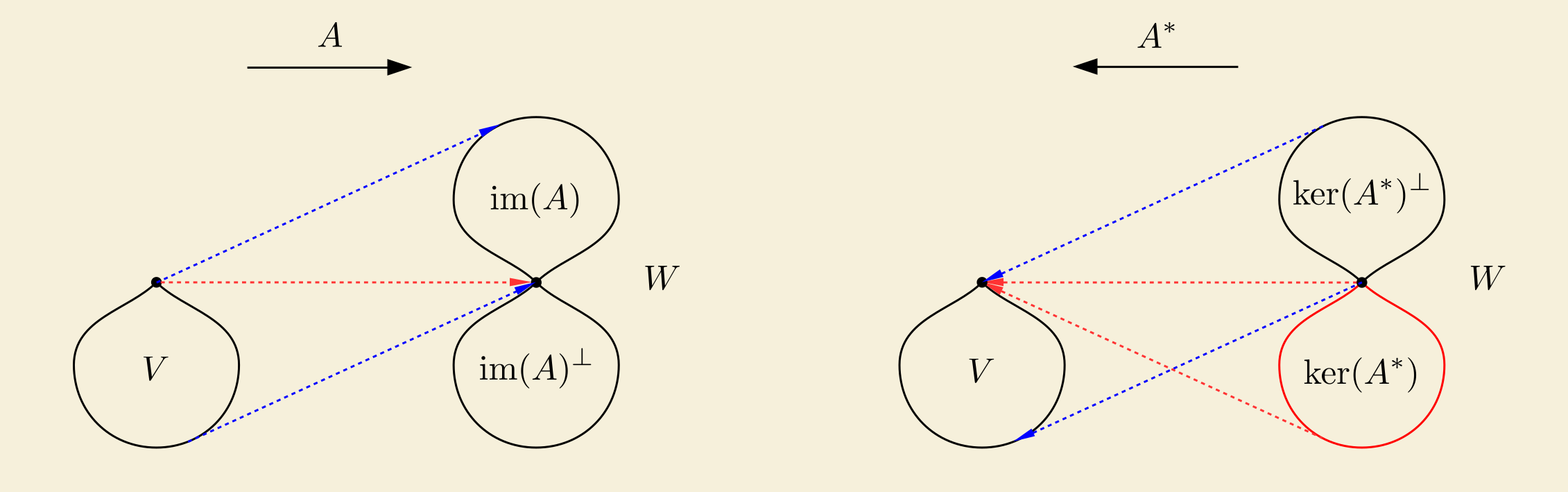
  • When a matrix \(A\) has full column rank \(r=n\):

    • The linear map represented by \(A\) is injective.
    • The linear map represented by \(A^{\ast}\) is surjective.
    • \(A\) has a left inverse and \(A^{\ast}\) has a right inverse.

    img

  • General case

    We have

    \[\begin{equation} \begin{aligned} \mathrm{Im}(A) &= \left( \mathrm{ker}(A^{\ast}) \right)^{\perp} \\ \mathrm{Im}(A^{\ast}) &= \left( \mathrm{ker}(A) \right)^{\perp} \end{aligned}. \end{equation}\]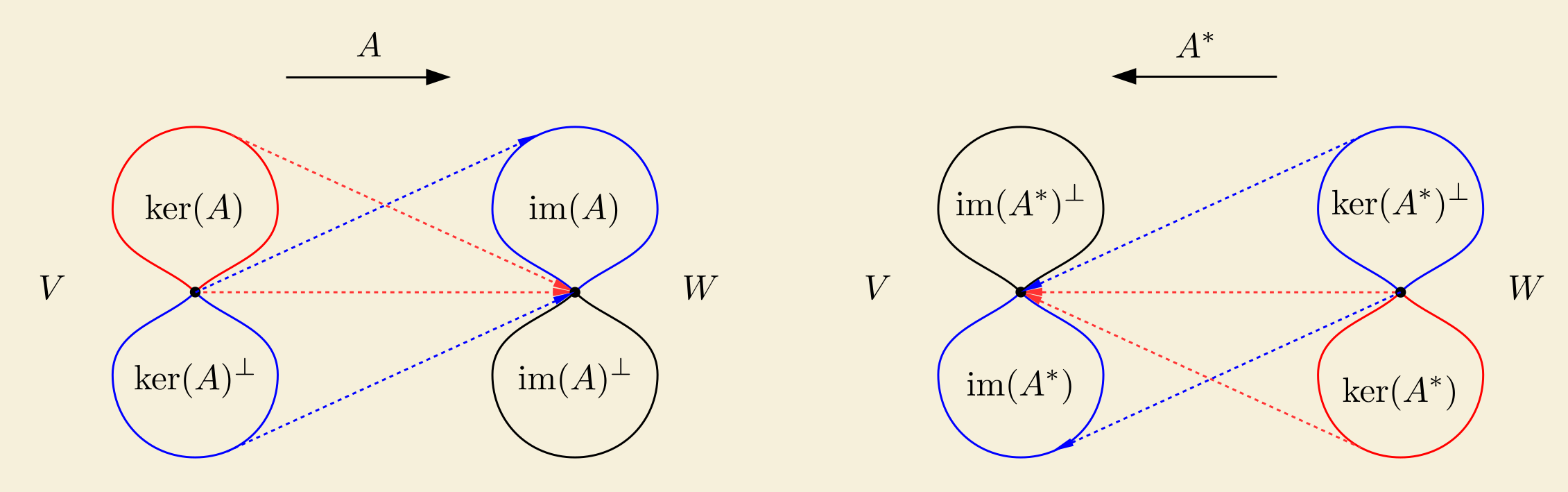

    img

Backlinks: 《Moore-Penrose pseudoinverse and generalized inverse》