Variational problems

Contents

 1 Basic ideas
 2 When there is no constraint
  2.1 Preconditions
  2.2 Problem definitions
  2.3 Unique solvability and stability
 3 When there is a constraint \(Bu=g\)
  3.1 Preconditions
  3.2 Problem definitions
  3.3 Unique solvability and stability

1 Basic ideas

• There are three types of problems:

  • The original operator equation \(Au=f\). The two sides of this equation are functions and should be equal pointwise. This is the strong form problem.

  • The variational problem is obtained by projecting the two sides of the operator equation to a test function space \(V\). The “projection” here means multiply the two sides of the equation with an arbitrary function in the test function space, then integrate them over the domain, i.e. \(\left \langle Au,v \right \rangle =\left \langle f,v \right \rangle \). Therefore, infinitely many equations are established and we say the equality is in the sense of projection. This is the weak form problem.

    We can also understand the test function space \(V\) as a multidimensional ruler. The right hand side function \(f\) of the operator equation and the output function returned from applying the partial differential operator to the solution function, i.e. \(Au\), will be measured with this ruler.

  • The problem of minimizing an energy functional, such as \(\mathcal {L}(v)=\frac {1}{2}\left \langle Av,v \right \rangle -\left \langle f,v \right \rangle \).

• The operator equation and the variational problem is equivalent due to the boundedness of the bilinear form \(a(u,v):= \left \langle Au,v \right \rangle \).

• The variation problem is further equivalent to the minimization problem, if the bilinear form \(a(u,v)\) is symmetric and positive definite. This condition is equivalent to that the linear operator \(A\) associated with this bilinear form \(a(u,v)\) is self-dual and elliptic. Of course, the boundedness of the bilinear form \(a(u,v)\) is equivalent to the boundedness of the linear operator \(A\).

2 When there is no constraint

2.1 Preconditions

• \(X\) is a Hilbert space and \(X'\) is the dual space of \(X\).

• \(\left \langle \cdot ,\cdot \right \rangle _X\) is the inner product in \(X\).

• \(\left \langle \cdot ,\cdot \right \rangle \) is the duality pairing, which applies a linear functional \(f\in X'\) to an element \(u\in X\), i.e. \(\left \langle f,u \right \rangle =\left \langle u,f \right \rangle =f(u)\).

• \(A: X \rightarrow X'\) is a bounded linear operator satisfying \begin{equation} \norm {Av}_{X'}\leq c_2^A\norm {v}_X \quad \forall v \in X. \end{equation}

• \(f\in X'\)

2.2 Problem definitions

Definition 1 (Operator equation with no constraint) Find \(u \in X\) satisfying \begin{equation} Au = f. \end{equation}

Definition 2 (Variational problem with no constraint) Find \(u\in X\) such that \begin{equation} \left \langle Au,v \right \rangle = \left \langle f,v \right \rangle \quad \forall v\in X. \end{equation}

Definition 3 (Minimization problem for no constraint case) Let \(F\) be the functional \begin{equation} F(v) := \frac {1}{2}\left \langle Av,v \right \rangle - \left \langle f,v \right \rangle \quad (v\in X). \end{equation} The minimization problem is defined as \begin{equation} F(u) =\min _{v\in X} F(v). \end{equation}

Relations between the above problems:

• Operator equation (Definition 1) \(\Longleftrightarrow \) variational problem (Definition 2)

• When \(A\) is further self-adjoint ¹ and positive semi-definite, variational problem (Definition 2) \(\Longleftrightarrow \) minimization problem (Definition 3)

2.3 Unique solvability and stability

The unique solvability of the operator equation (Definition 1) (and thus the variational problem (Definition 2)) for any \(f\in X'\) is governed by the Lax-Milgram Lemma, which requires that \(A\) should be \(X\)-elliptic, i.e. \begin{equation} \label {eq:ellipticity-condition} \left \langle Av,v \right \rangle \geq c_1^A\norm {v}_X^2 \quad \forall v\in X. \end{equation} It also prescribes a stability condition on the solution \(u\): \begin{equation} \norm {u}_X\leq \frac {1}{c_1^A}\norm {f}_{X'}. \end{equation} It can be seen that the smaller the ellipticity constant \(c_1^A\), the less the stability for \(u\). \(c_1^A\) is related to the smallest eigenvalue of the discretized matrix for the operator \(A\). A small \(c_1^A\) is caused by an increase in the number of DoFs and sharp corners in the geometry of the model. The error in the data for \(f\) will be amplified by \(\frac {1}{c_1^A}\).

Remark 1 (Understanding about ellipticity of operators) We are going to compare the ellipticity condition in Equation (6) with its discrete counterpart. Let \(\mathscr {A}\) be the matrix in \(\mathbb {R}^{n\times n}\) corresponding to \(A\) which is discretized via the Galerkin method. Let \(x\) be the vector in \(\mathbb {R}^n\) related to \(v\). Assume \(\mathscr {A}\) has \(n\) eigenvalues \(\lambda _1,\cdots ,\lambda _n\) and \(n\) eigenvectors \(v_1,\cdots ,v_n\) (N.B. Even though the multiplicity of some of the eigenvalues may be larger than one, for the same number of eigenvectors spanning its eigenspace, we can still explicitly use different symbols to represent their same eigenvalue. Therefore, we allow duplicated values in the list \(\lambda _1,\cdots ,\lambda _n\). Because the sum of the multiplicity of all eigenvalues is \(n\) and all the eigenspaces are orthogonal to each other, we can choose those eigenvectors \(v_1,\cdots ,v_n\) to form an orthonormal set. Then any vector \(x\) in \(\mathbb {R}^n\) can be expanded by this basis: \begin{equation} x = \sum _{i=1}^n c_i v_i. \end{equation} And the duality pairing can be represented as \begin{equation} x^{\mathrm {T}} \mathscr {A} x = \left ( \sum _{i=1}^n c_iv_i^{\mathrm {T}} \right ) \mathscr {A} \left ( \sum _{j=1}^n c_jv_j \right ) = \sum _{i,j} c_ic_j v_i^{\mathrm {T}} \mathscr {A} v_j = \sum _{i,j} c_ic_j \lambda _j (v_i,v_j), \end{equation} where \((\cdot ,\cdot )\) is the inner product in \(\mathbb {R}^n\). Because \(v_1,\cdots ,v_n\) are orthonormal, we have \((v_i,v_j) =\delta _{ij}\). Hence, \begin{equation} x^{\mathrm {T}} \mathscr {A} x = \sum _{i=1}^n \lambda _i c_i^2. \end{equation} If \(\mathscr {A}\) is positive definite, the solution to the linear system \(Ax = b\) exists and is unique. Since all eigenvalues of \(\mathscr {A}\) are larger than zero, we let \(\lambda _{\min }\) be the minimum and then have \begin{equation} \left ( \mathscr {A}x, x \right ) = x^{\mathrm {T}} \mathscr {A} x \geq \lambda _{\min } \sum _{i=1}^n c_i^2 = \lambda _{\min } \lVert x \rVert _{\mathbb {R}^n}^2. \end{equation} We can see that this discrete formulation is consistent with the ellipticity condition. The ellipticity constant \(c_1^A\) of the bounded linear operator \(A\) corresponds to the minimum eigenvalue of the positive definite matrix \(\mathscr {A}\). That’s why the ellipticity condition is the key in the Lax-Milgram Lemma, which governs the existence and uniqueness of the solution for a PDE formed by \(A\).

3 When there is a constraint \(Bu=g\)

3.1 Preconditions

• \(X\) and \(\Pi \) are Banach spaces ² with their dual spaces \(X'\) and \(\Pi '\).

• \(A: X \rightarrow X'\) is a bounded linear operator satisfying \begin{equation} \norm {Av}_{X'}\leq c_2^A\norm {v}_X \quad \forall v \in X. \end{equation}

• \(B: X \rightarrow \Pi '\) is a bounded linear operator satisfying \begin{equation} \norm {Bv}_{\Pi '} \leq c_2^B\norm {v}_X \quad \forall v\in X. \end{equation}

• \(B': \Pi \rightarrow X'\) is the adjoint operator of \(B\) ³.

• \(f\in X'\) and \(g \in \Pi '\)

The relationship between various spaces is illustrated in Figure 1, where \(J_X\) and \(J_{\Pi }\) are Riesz maps ⁴.

Figure 1: Relationship between various spaces in the variational problem.

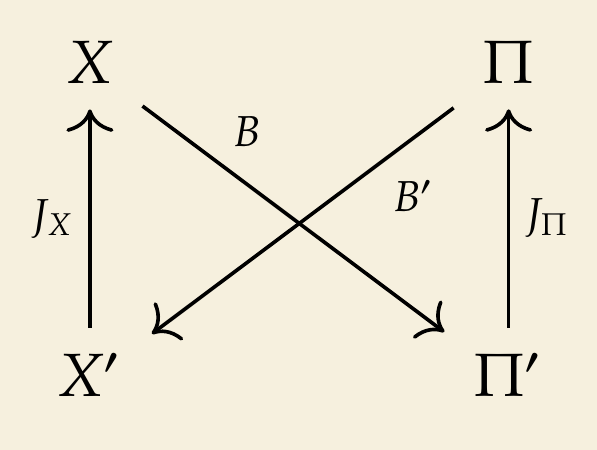
3.2 Problem definitions

Definition 4 (Operator equation with constraint \(Bu=g\)) Define the manifold \(V_g := \left \{ v\in X: Bv=g \right \}\) and the kernel space \(V_0 := \ker B\). Assume the solvability condition \(g\in \image _XB\) and \(f\in \image _{V_g}A\). Then find \(u\in V_g\) satisfying \begin{equation} Au = f. \end{equation} N.B. If we require \(u\) to be within the space \(V_g\), the constraint \(Bu=g\) is automatically satisfied.

Definition 5 (Variational problem with constraint \(Bu=g\)) Assume the solvability condition \(g\in \image _XB\) and \(f\in \image _{V_g}A\). Then find \(u\in V_g\) satisfying \begin{equation} \left \langle Au,v \right \rangle = \left \langle f,v \right \rangle \quad \forall v\in V_0. \end{equation}

Remark 2 Such constraint \(Bu=g\) can be the essential boundary condition, i.e. Dirichlet boundary condition. Then the solution \(u\) is sought in the space \(V_g\) which explicitly satisfies the Dirichlet boundary condition, while the test function is chosen from the space \(V_0\) which satisfies the homogeneous Dirichlet boundary condition.

Definition 6 (Extended variational problem using Lagrange multiplier) Introduce the Lagrange multiplier \(p\in \Pi \). Find \((u,p)\in X\times \Pi \) such that \begin{equation} \begin {aligned} \left \langle Au,v \right \rangle + \left \langle Bv,p \right \rangle &= \left \langle f,v \right \rangle \\ \left \langle Bu,q \right \rangle &= \left \langle g,q \right \rangle \end {aligned} \quad \forall (v,q)\in X\times \Pi . \end{equation}

Remark 3 The solution \((u,p)\) is sought in the product space \(X \times \Pi \) but not \(V_g \times \Pi \).

Definition 7 (Saddle point problem related to the variational problem with constraint in Definition 5) Let \(\mathcal {L}\) be the Lagrange functional \begin{equation} \mathcal {L}(v,q) := \frac {1}{2}\left \langle Av,v \right \rangle - \left \langle f,v \right \rangle + \left \langle Bv,q \right \rangle - \left \langle g,q \right \rangle \quad (v,q)\in X\times \Pi . \end{equation} The saddle point problem is defined as: find \((u,p)\in X\times \Pi \) such that \begin{equation} \mathcal {L}(u,q)\leq \mathcal {L}(u,p)\leq \mathcal {L}(v,p) \quad \forall (v,q)\in X\times \Pi . \end{equation}

Relations between the above problems

• Operator equation with constraint (Definition 4) \(\Longleftrightarrow \) variational problem with constraint (Definition 5)

• Variation problem with constraint (Definition 5) \(\Longleftrightarrow \) extended variational problem using Lagrange multiplier (Definition 6)

• When \(A\) is further self-adjoint and positive semi-definite, extended variational problem using Lagrange multiplier (Definition 6) \(\Longleftrightarrow \) saddle point problem (Definition 7)

3.3 Unique solvability and stability

• The unique solvability of the variational problem (Definition 5) (and thus the operator equation (Definition 4)) for any \(f\in \image _{V_g}A\) and \(g\in \image _XB\) is ensured when \(A\) is \(V_0\)-elliptic, \begin{equation} \left \langle Av,v \right \rangle \geq c_1^A\norm {v}_X^2 \quad \forall v\in V_0 := \kernel B. \end{equation} This can be considered as an extension of the Lax-Milgram Lemma. If we further assume a condition on the constraint \(Bu=g\) relation: for any \(g\in \image _XB\), there exists a \(u_g\in V_g\) such that \begin{equation} \label {eq:ug-norm-constraint} \norm {u_g}_X \leq c_B \norm {g}_{\Pi '}, \end{equation} which can be considered as a stability condition on \(u_g\) derived from the constraint relation only (or we say the norm of the function \(u_g\) is controlled by the norm of the given data \(g\)), then the following stability condition holds for the unique solution \(u\) of the variational problem (Definition 5) or the operator equation (Definition 4): \begin{equation} \norm {u}_X \leq \frac {1}{c_1^A}\norm {f}_{X'} + \left ( 1+\frac {c_2^A}{c_1^A} \right ) c_B \norm {g}_{\Pi '}. \end{equation} From this we can see that the stability of \(u\) is better when the \(V_0\)-ellipticity constant \(c_1^A\) is larger, the boundedness constant \(c_2^A\) of \(A\) is smaller and the stability constant \(c_B\) for \(u_g\) is smaller. It is obvious that when the operator \(A\) is unbounded, the solution \(u\) is unstable. Therefore, the boundedness of \(A\) is very important.

• The unique solvability of the extended variational problem using Lagrange multiplier (Definition 6) can be achieved for any \(f\in \image _{V_g}A\) and \(g\in \image _XB\), when \(V_0\)-ellipticity for \(A\), stability condition for \(u_g\in V_g\) as in (20) and the stability condition for \(q\in \Pi \) \begin{equation} \label {eq:stability-for-q} c_S\norm {q}_{\Pi }\leq \sup _{0\neq v\in X}\frac {\abs {\left \langle Bv,q \right \rangle }}{\norm {v}_X} \quad (\forall q\in \Pi ) \end{equation} are satisfied. Since \begin{equation} \sup _{0\neq v\in X}\frac {\abs {\left \langle Bv,q \right \rangle }}{\norm {v}_X} = \sup _{0\neq v\in X}\frac {\abs {\left \langle v,B'q \right \rangle }}{\norm {v}_X} = \norm {B'q}_{X'}\leq \norm {B'}\norm {q}_{\Pi }, \end{equation} the stability condition for \(q\) in (22) is equivalent to \begin{equation} \norm {B'}\geq c_S, \end{equation} which means the norm of the adjoint operator \(B'\) should have a non-zero lower bound.

  Then the stability conditions for the solution \((u,p)\in X\times \Pi \) are \begin{equation} \norm {u}_X\leq \frac {1}{c_1^A}\norm {f}_{X'}+\left ( 1+\frac {c_2^A}{c_1^A} \right )c_B\norm {g}_{\Pi '} \end{equation} and \begin{equation} \norm {p}_{\Pi }\leq \frac {1}{c_S} \left ( 1+\frac {c_2^A}{c_1^A} \right ) \left \{ \norm {f}_{X'}+c_Bc_2^A\norm {g}_{\Pi '} \right \}. \end{equation} It can be seen that the larger the lower bound \(c_S\) for \(\norm {B'}\), the larger the stability for \(p\).

• The unique solvability of the extended variational problem using Lagrange multiplier (Definition 6) can also be achieved for any \(f\in X'\) and \(g\in \Pi '\), when \(X\)-ellipticity for \(A\), i.e. \begin{equation} \left \langle Av,v \right \rangle \geq c_1^A\norm {v}_X^2 \quad \forall v\in X, \end{equation} and the stability condition for \(q\in \Pi \) as in (22) are satisfied. The stability conditions for the solution \((u,p)\in X\times \Pi \) are \begin{equation} \norm {u}_X\leq \frac {1}{c_1^A}\left ( 1+\frac {(c_2^B)^2}{c_1^Ac_1^S} \right )\norm {f}_{X'}+\frac {c_2^B}{c_1^Ac_1^S}\norm {g}_{\Pi '} \end{equation} and \begin{equation} \norm {p}_{\Pi }\leq \frac {1}{c_1^S}\norm {BA^{-1}f-g}_{\Pi '}\leq \frac {1}{c_1^S}\left [ \frac {c_2^B}{c_1^A}\norm {f}_{X'}+\norm {g}_{\Pi '} \right ], \end{equation} where \(c_1^S\) is the coefficient for the \(\Pi \)-ellipticity of the operator \(S := BA^{-1}B': \Pi \rightarrow \Pi '\), i.e. \begin{equation} \left \langle Sq,q \right \rangle \geq c_1^S \norm {q}_{\Pi }^2 \quad \forall q\in \Pi . \end{equation} This \(\Pi \)-ellipticity depends on the \(V_0\)-ellipticity for \(A\) and the stability condition for \(q\) as in (22).

References

   Olaf Steinbach. Numerical Approximation Methods for Elliptic Boundary Value Problems: Finite and Boundary Elements. Springer Science & Business Media. ISBN 978-0-387-31312-2.

¹In (Steinbach), self-adjoint is actually self-dual in functional analysis.

²In Banach spaces, inner product is not defined, so according to functional analysis, the concept of adjointness is not available. This again verifies my understanding that in (Steinbach), self-adjoint is actually self-dual.

³In functional analysis, this is actually the dual operator, not adjoint operator.

⁴N.B. A Riesz map maps from the dual space to the primal space.