Understanding about the orientation dependence of pseudo differential forms
Consider a \(d\)-dimensional manifold \(M^d\) with two overlapping coordinate charts \((U, u)\) and \((V,v)\). Both of them are orthonormal and \((V,v)\) has a different orientation from \((U,u)\). Let \(o(\cdot)\) be the orientation function which returns 1 or -1 for a coordinate chart. Then \(o(v) = -o(u)\).
In \((U,u)\), when the full degree differential form \(du^1\wedge \cdots \wedge du^n\) is applied to an \(n\)-vector \((v_1,\cdots,v_n)\) rooted at a point \(p\) in \(U\cap V\), the returned scalar is the signed volume spanned by the \(n\)-vector. To measure the signed volume in the coordinate chart \((V,v)\), we still apply the full degree differential from \(dv^1\wedge\cdots\wedge dv^n\) to \(v_1,\cdots,v_n\). Then the returned volume must have a different sign from that using \((U,u)\), because \(o(v) = -o(u)\). N.B. Even though the \(n\)-vector has different numerical representations in these two coordinate charts, it is a fixed physical entity in the space.
Because the \(n\)-vector is a fixed entity, we want to make the two returned scalar values consistent under different coordinate charts. To make the returned volume not dependent on the orientation, we need to make the full degree differential form orientation dependent by adding the orientation function \(o(\cdot)\) as a factor. In this way, we obtain the volume form for an arbitrary coordinate chart \((u)\) as
\[\begin{equation} \mathrm{vol}_u^n = o(u) du^1\wedge\cdots\wedge du^n. \end{equation}\]N.B. The indices of the basis elements in the wedge product must be in an increasing order. Because the volume form is made orientation dependent to ensure its measurement of signed volume compatible in different coordinate charts, it is different from a normal differential form and is called a pseudo form.
Take the Cartesian space \(\mathbb{R}^3\) as an example.
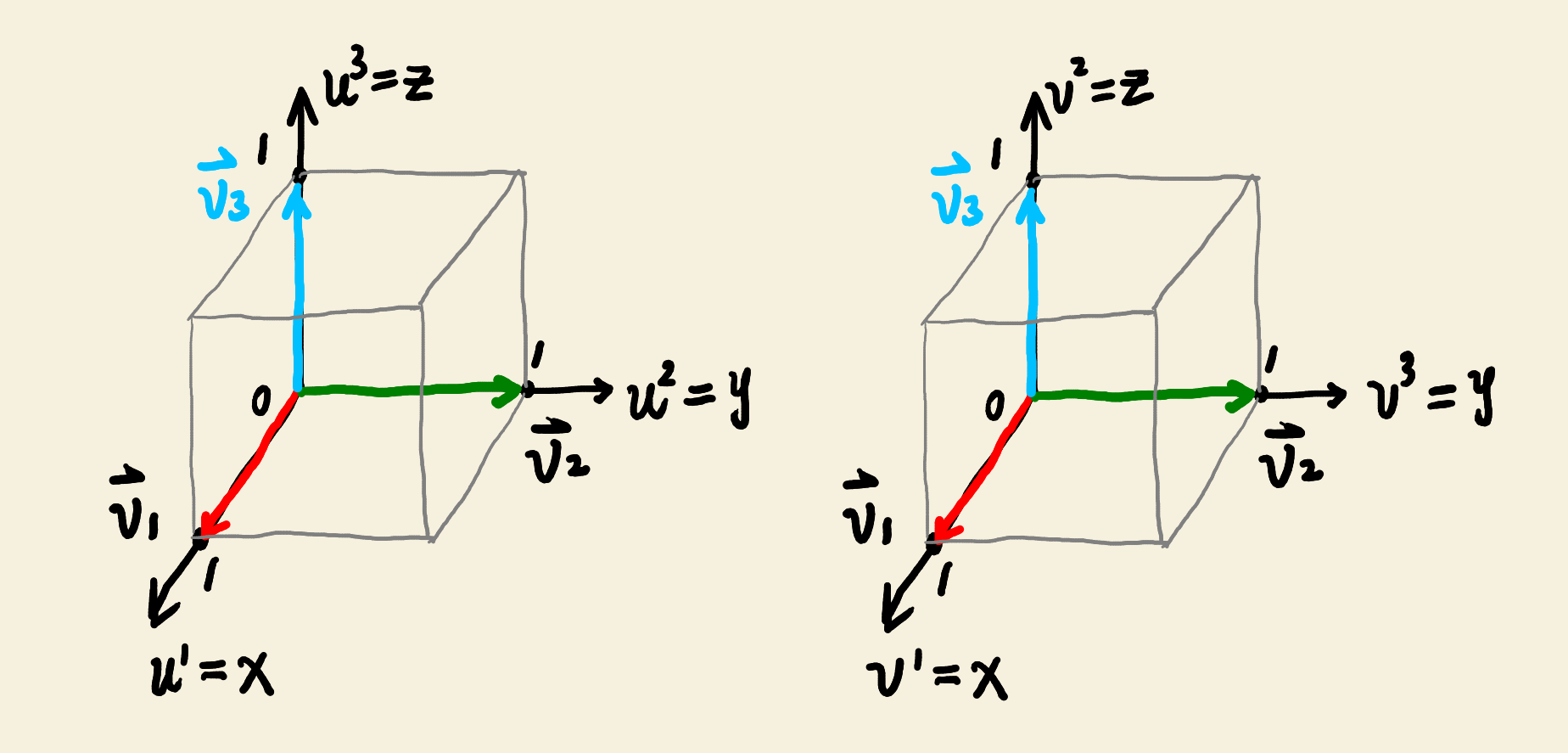
As a convention, we adopt the frame \((u) = (x, y, z)\) with the right handedness and assume that \(o(u) = 1\). The volume form is \(\mathrm{vol}_u^3 = o(u) dx\wedge dy \wedge dz = dx\wedge dy \wedge dz\). Then we want to get the signed volume spanned by the basis vectors of the three axes, \(\boldsymbol{v}_1 = (1,0,0)\), \(\boldsymbol{v}_2 = (0,1,0)\) and \(\boldsymbol{v}_3 = (0,0,1)\). We have
\[\begin{equation} \mathrm{vol}_u^3(\boldsymbol{v}_1,\boldsymbol{v}_2,\boldsymbol{v}_3) = \det \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix} = 1. \end{equation}\]If we choose another frame \((v) = (x, z, y)\) with a different orientation \(o(v)=-1\) by swapping \(y\) and \(z\) coordinates, the volume form becomes
\[\begin{equation} \label{eq:volume-form-in-v} \mathrm{vol}_v^3 = o(v) dv^1\wedge dv^2 \wedge dv^3 = -dv^1\wedge dv^2 \wedge dv^3. \end{equation}\]In this new chart, the 3-vector becomes \(\boldsymbol{v}'_1 = (1,0,0)\), \(\boldsymbol{v}'_2 = (0,0,1)\) and \(\boldsymbol{v}'_3 = (0,1,0)\). Then the signed volume spanned by them is
\[\begin{equation} \mathrm{vol}_v^3(\boldsymbol{v}'_1,\boldsymbol{v}'_2,\boldsymbol{v}'_3) = -\det \begin{pmatrix} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{pmatrix} = 1. \end{equation}\]So the returned volume in \((V,v)\) is the same as that in \((U,u)\).
If we substitute \((x, z, y)\) for \(v^1,v^2,v^3\) in Equation \eqref{eq:volume-form-in-v}, using the anti symmetry of wedge product,
\[\begin{equation} \mathrm{vol}_v^3 = -dx\wedge dz \wedge dy = dx\wedge dy \wedge dz = \mathrm{vol}_u^3, \end{equation}\]we find out \(\mathrm{vol}_v^3\) is just equivalent to \(\mathrm{vol}_u^3\).
Also note that for a given pseudo form, with the anti symmetry of wedge product, we can arbitrarily change the order of basis elements in the wedge product \(du^1\wedge\cdots\wedge du^n\) while keeping the differential form unchanged, as long as we add a factor \((-1)^m\) to it, where \(m\) is the number of permutations. However, such an operation has nothing to do with the orientation of the local coordinate chart, since the chart does not change in this process. So this is only an algebraic operation.