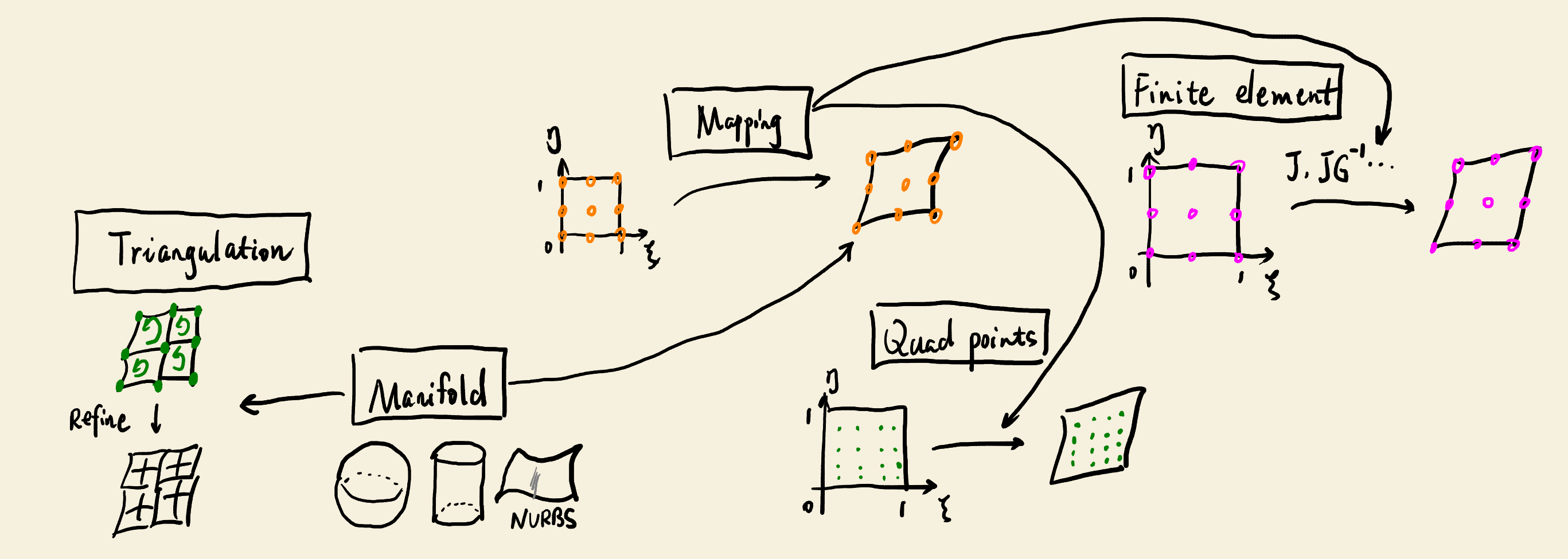
The interplay between triangulation, manifold, mapping, quadrature point and finite element
In FEM or BEM, the five entities, namely triangulation, manifold, mapping, quadrature point and finite element, work together to discretize the spatial domain and prepare necessary data for cellwise computation. This article explains their functions and relationships.
-
Triangulation
A triangulation describes the topological relationship between vertices and cells. It contains these data:
- Coordinates for vertices
- A cell is represented as an ordered list of vertex indices. This order is consistent with the normal direction of the cell and the cell normal inherits from the normal direction of the geometric entity to which the cell belongs.
-
Manifold
A manifold is used to generate new geometry-conforming points in a cell in the triangulation. For example, two vertices defines an edge of a cell and a new point in the middle of this edge is computed as a weighted average of the two vertices. Similarly, given four vertices of a quadrangular cell, a new point in the center of this cell is computed as a weighted average of the four vertices.
Generating new points in a cell is needed in two cases:
- Mesh refinement
- Define the support points of mapping shape functions, if the Lagrange type mapping is adopted.
-
Mapping
A mapping object has two purposes:
- Defines a map from the unit/reference cell to a real cell. When coming to a different real cell in the triangulation, the mathematical function implied by this map changes because the coordinates of the cell vertices are different. With the language of differential geometry, the mapping object assigns a locate coordinate chart to each cell in the triangulation. The local coordinate charts from all cells form an atlas over the triangulation.
- Compute quantities such as Jacobian matrices and determinants, normal vectors and covariant transformation matrices, etc.
- A Jacobian matrix is used to transform a tangent vector from the local coordinate chart to the global Cartesian frame.
- The Jacobian determinant is used when an integral is pulled back from the global Cartesian frame to the local coordinate chart.
- For a surface cell with a manifold dimension 2 and a spatial dimension 3, the normal vector at a point in this cell is the cross product of the two basis vectors for the local coordinate chart. Some BEM kernel functions such as the double layer kernel and its adjoint need the normal vector information.
-
The covariant matrix is used to transform a gradient vector from the local coordinate chart to the global Cartesian frame. The procedure is
- Transform the 1-form in the local coordinate chart to tangent vector via the inverse of the metric tensor $G^{-1} $.
- Push forward the tangent vector in the local coordinate chart to the global Cartesian frame via the Jacobian matrix $J $.
The total transformation is the covariant matrix $J G^{-1} $.
Examples of mapping objects:
-
Lagrange type mapping
It uses Lagrange polynomials as shape functions to construct the map from the unit cell to a real cell. The non-zero part of each shape function concentrates around a support point. Therefore, the higher the order of the polynomials, the more the shape functions and hence the more the support points. When the polynomial order is 1, i.e. the map is linear, the four vertices of a cell are just the support points of all the four shape functions. When the polynomial order is larger than 1, more support points are needed which are located either in the middle of edges or in the cell interior. As mentioned above, the generation of these intermediate support points needs to consult the manifold object.
-
Manifold conforming mapping
In this case, the map from the unit cell to a real cell conforms exactly with the manifold. The computation of quantities such as Jacobian matrices and determinants etc. will depend on how the manifold is defined.
-
Quadrature points
Quadrature points are generated in the unit cell. With a mapping object, they can be transformed to points in a real cell.
-
Finite element
The evaluation of the shape functions and their derivatives for a finite element is performed at all quadrature points in the unit cell. These are fixed values, which can be precomputed and stored. The vector forms of differential forms in the global Cartesian frame can be computed from these fixed values and transformed to a real cell with the help of the mapping object. And the mapping object further depends on the manifold object.