Shape functions and basis functions in FEM

According to my graduate student experience, the difference between shape functions and basis functions in FEM was not clarified in my numerical method course. Therefore, in this article, I illustrate and explain this point with the help of the symbolic math software Maxima.

1 Lagrange polynomials as shape functions on reference cells

Load packages.

(%i1)

kill(all)$

(%i6)

load("eigen")$ load("fem.mac")$ load("draw")$ load("color_map.mac")$ load("mnewton")$ load("tex_format.mac")$

Plot configurations

(%i12)

fig_size : [1280,1024]$ wxplot_size : fig_size$ fig_font : "Helvetica"$ fig_font_size : 20$ wxanimate_autoplay : false$ wxanimate_framerate : 1$

1.1 1D

Generate the four 3rd order Lagrange polynomials on $[0, 1]$.

(%i13)

reference_cell_1d : [0, 1]$

(%i14)

support_points_1d : GenLagrangeNodes1D(3, reference_cell_1d);

\[\operatorname{(support\_ points\_ 1d) }\left[ 0\operatorname{,}\frac{1}{3}\operatorname{,}\frac{2}{3}\operatorname{,}1\right] \]

(%i16)

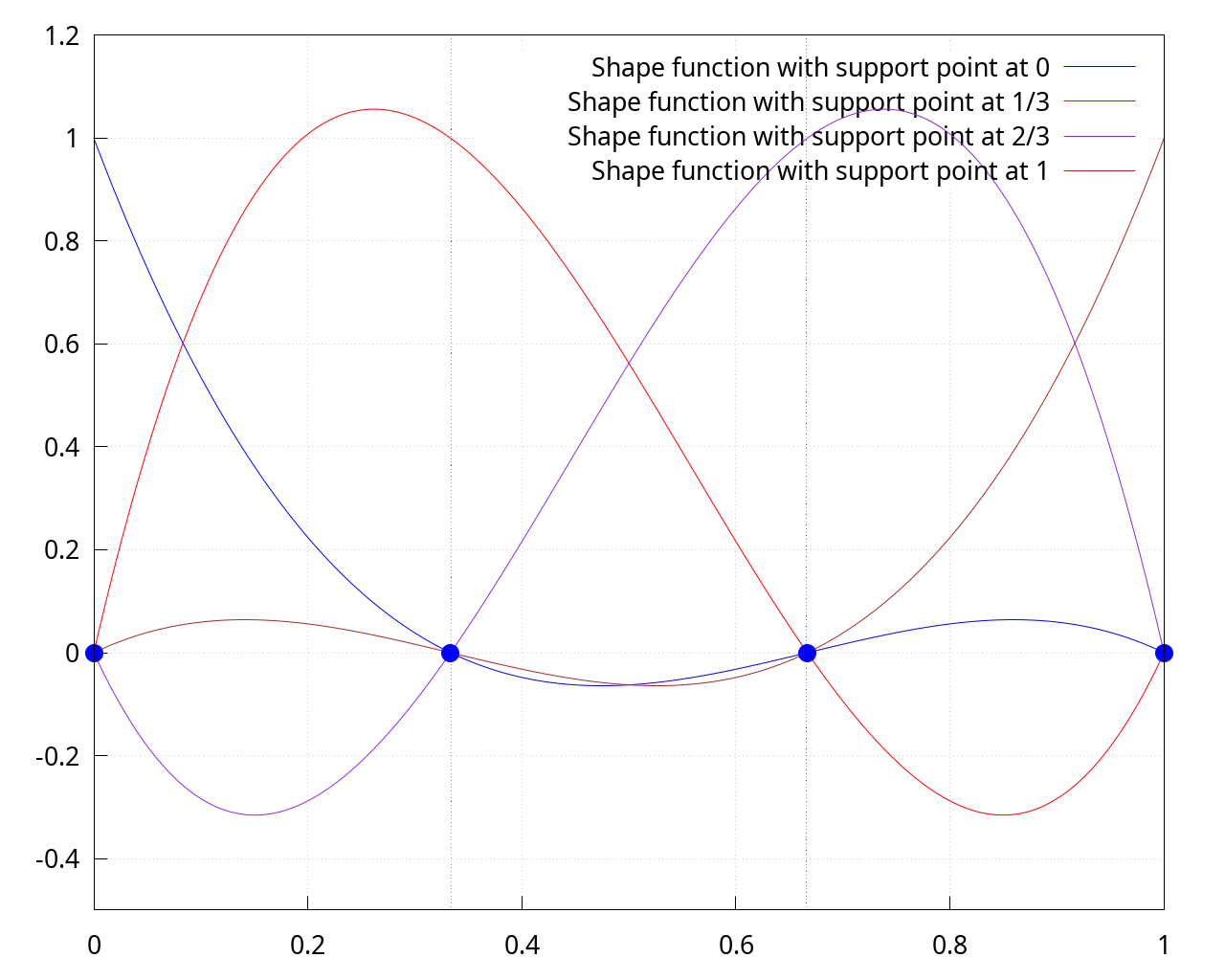
shape_functions_1d : GenLagrangeBases1D(3, reference_cell_1d, 'ξ)$ PrintEquationList(shape_functions_1d);

\[\]\[-\frac{9 \left( \xi -1\right) \, \left( \xi -\frac{2}{3}\right) \, \left( \xi -\frac{1}{3}\right) }{2} \]\[\frac{27 \left( \xi -1\right) \, \left( \xi -\frac{2}{3}\right) \xi }{2} \]\[-\frac{27 \left( \xi -1\right) \, \left( \xi -\frac{1}{3}\right) \xi }{2} \]\[\frac{9 \left( \xi -\frac{2}{3}\right) \, \left( \xi -\frac{1}{3}\right) \xi }{2}\]

We can see that a Lagrange polynomial is evaluated to 1 at its own support points and 0 at the support points of the other polynomails.

(%i17)

wxdraw2d(grid=true, xrange=reference_cell_1d, yrange=[-0.5, 1.2], dimensions=fig_size,    terminal=wxt, font=font_name, font_size=fig_font_size,    color=clist[1], key="Shape function with support point at 0",    explicit(shape_functions_1d[1], ξ, reference_cell_1d[1], reference_cell_1d[2]),    color=clist[2], key="Shape function with support point at 1/3",    explicit(shape_functions_1d[2], ξ, reference_cell_1d[1], reference_cell_1d[2]),    color=clist[3], key="Shape function with support point at 2/3",    explicit(shape_functions_1d[3], ξ, reference_cell_1d[1], reference_cell_1d[2]),    color=clist[4], key="Shape function with support point at 1",    explicit(shape_functions_1d[4], ξ, reference_cell_1d[1], reference_cell_1d[2]),    color=black, line_type = dots, key="",    implicit(x=support_points_1d[2], x, 0, 1, y, -0.5, 1.2),    color=black, line_type = dots, key="",    implicit(x=support_points_1d[3], x, 0, 1, y, -0.5, 1.2),    color=blue, point_type=filled_circle, point_size=3, points(makelist([support_points_1d[i],0], i, 1, 4)) );

1.2 2D

First, we generate two sets of 2nd order Lagrange polynomials in the 1D reference cell $[0, 1]$. Then by taking their tensor product, we can generate the 2nd order Lagrange polynomials on the 2D unit cell $[0, 1] \times [0, 1]$

(%i18)

support_points_2d : GenLagrangeNodes2D([2, 2], reference_cell_1d, reference_cell_1d);

\[\operatorname{(support\_ points\_ 2d) }\begin{pmatrix}0 & 0\\ \frac{1}{2} & 0\\ 1 & 0\\ 0 & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2}\\ 1 & \frac{1}{2}\\ 0 & 1\\ \frac{1}{2} & 1\\ 1 & 1\end{pmatrix}\]

(%i20)

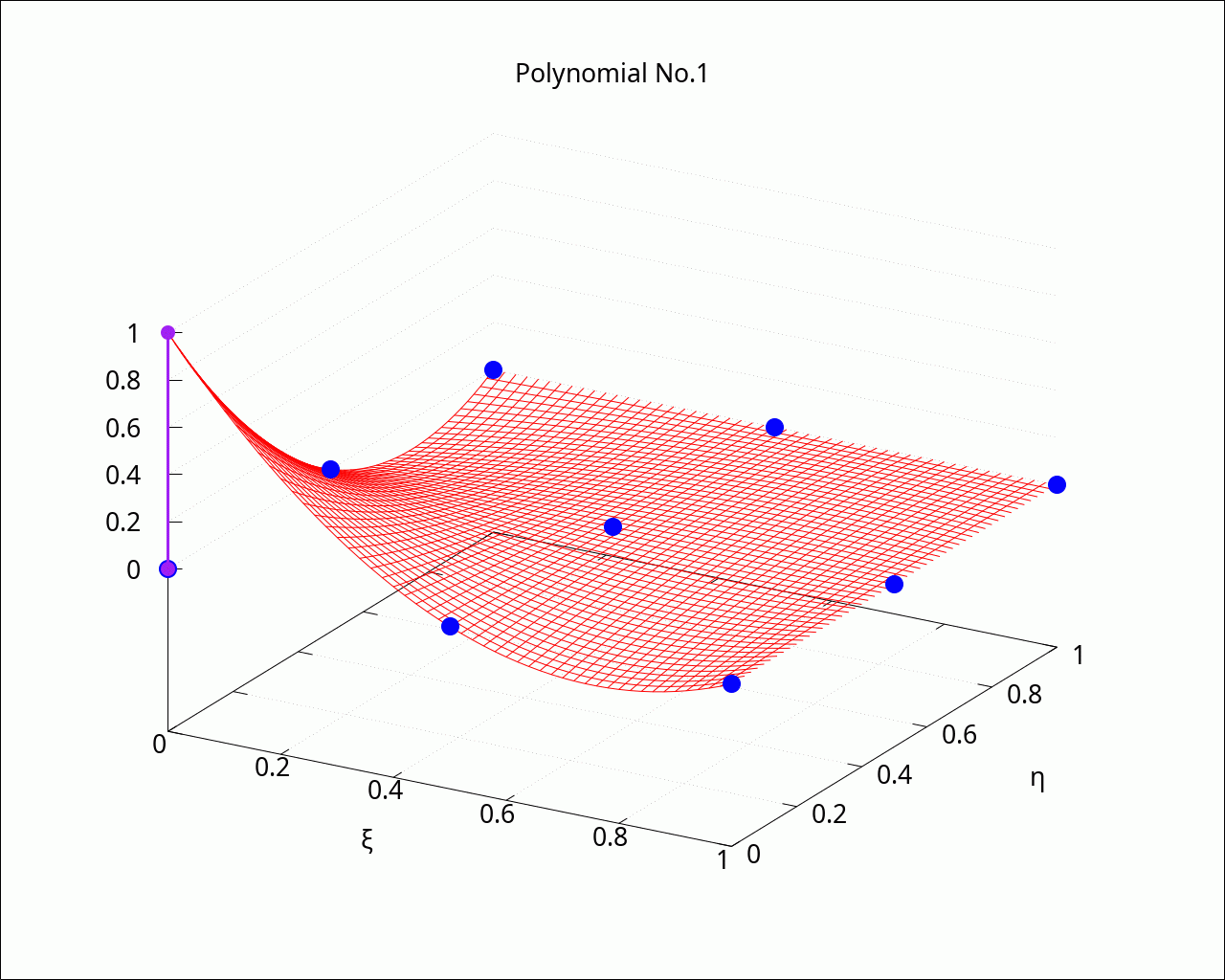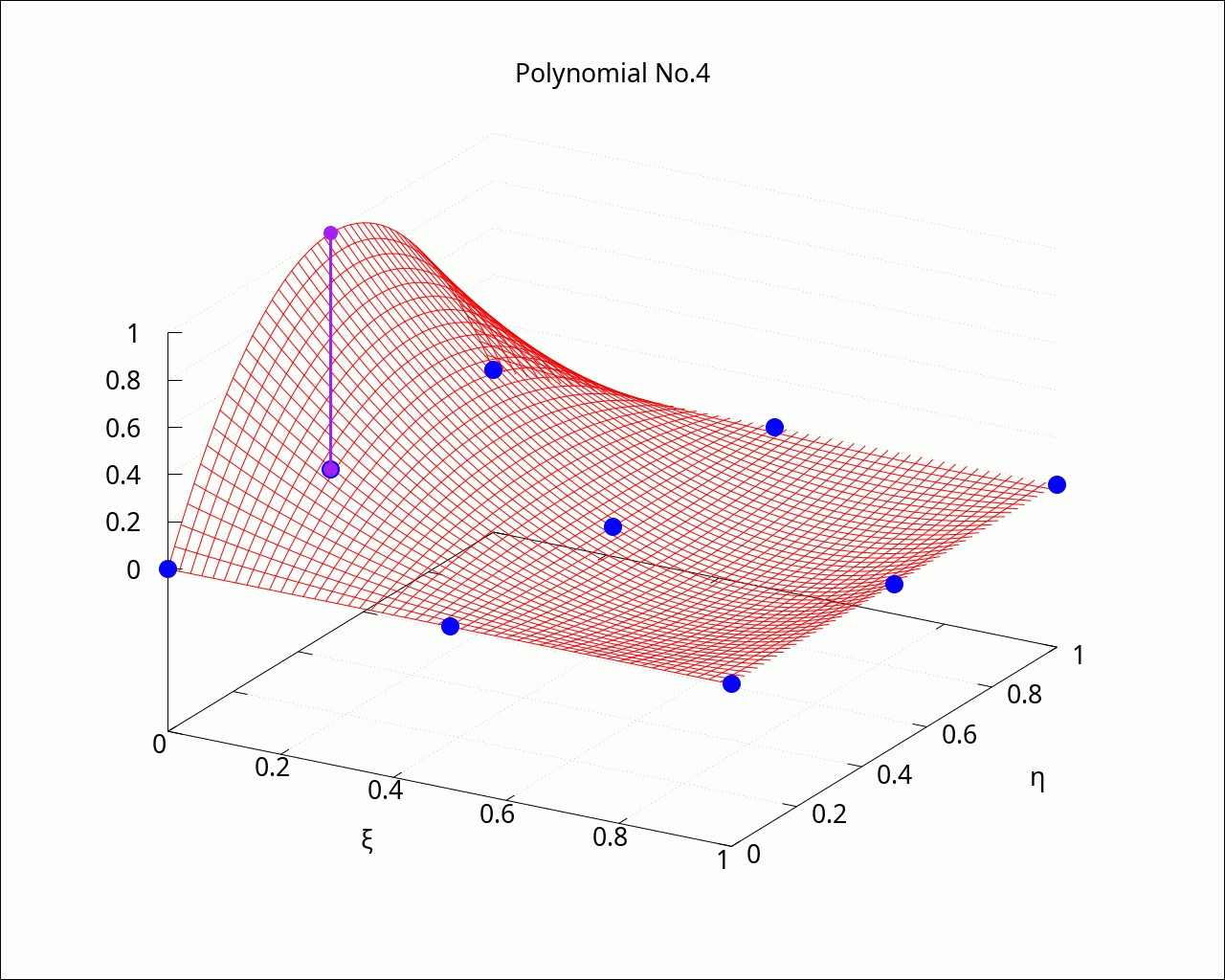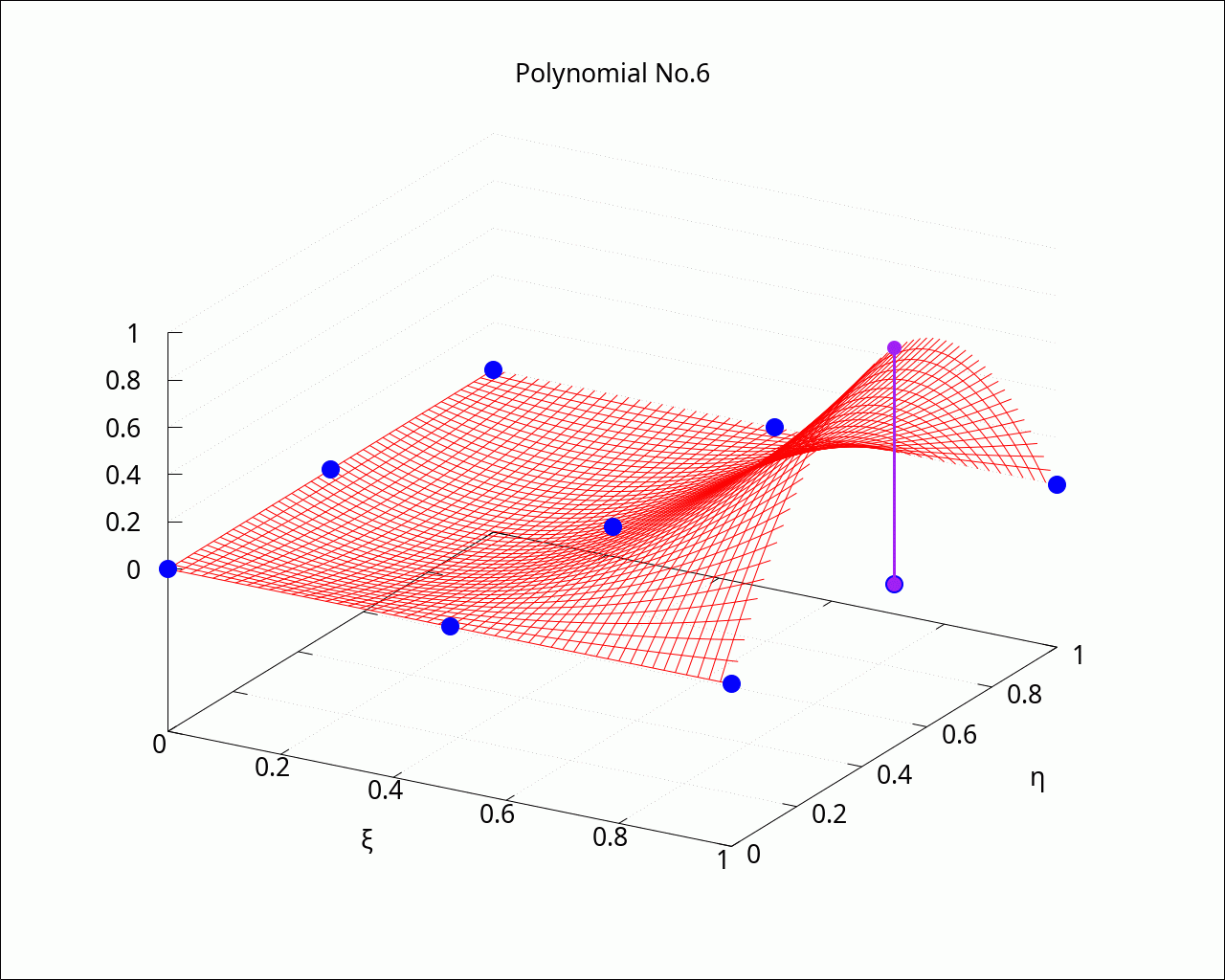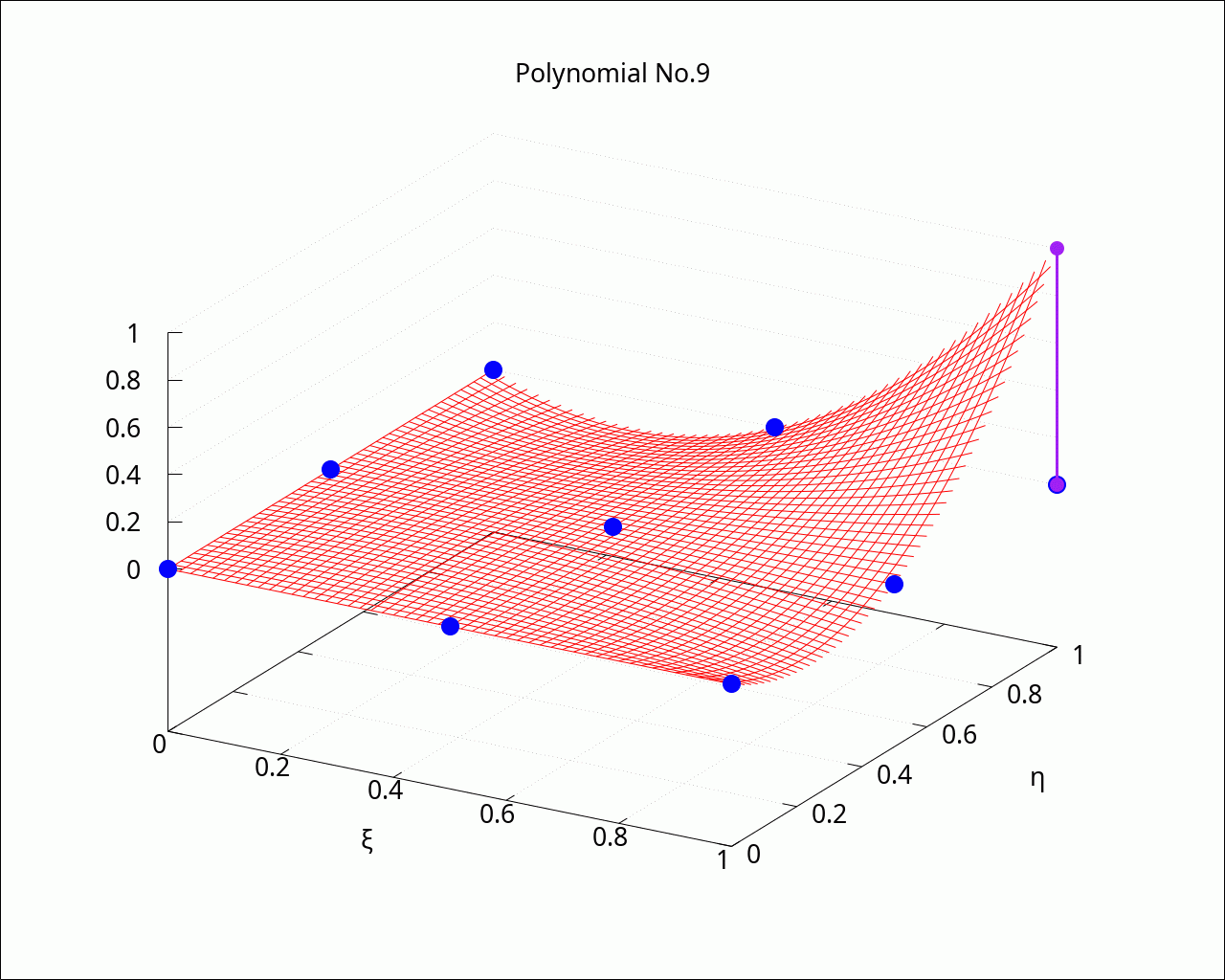
shape_functions_2d : GenLagrangeBases2D([2, 2], reference_cell_1d, reference_cell_1d, '[ξ, η])$ PrintEquationList(shape_functions_2d);

\[\]\[4 \left( \eta -1\right) \, \left( \eta -\frac{1}{2}\right) \, \left( \xi -1\right) \, \left( \xi -\frac{1}{2}\right) \]\[-8 \left( \eta -1\right) \, \left( \eta -\frac{1}{2}\right) \, \left( \xi -1\right) \xi \]\[4 \left( \eta -1\right) \, \left( \eta -\frac{1}{2}\right) \, \left( \xi -\frac{1}{2}\right) \xi \]\[-8 \left( \eta -1\right) \eta \, \left( \xi -1\right) \, \left( \xi -\frac{1}{2}\right) \]\[16 \left( \eta -1\right) \eta \, \left( \xi -1\right) \xi \]\[-8 \left( \eta -1\right) \eta \, \left( \xi -\frac{1}{2}\right) \xi \]\[4 \left( \eta -\frac{1}{2}\right) \eta \, \left( \xi -1\right) \, \left( \xi -\frac{1}{2}\right) \]\[-8 \left( \eta -\frac{1}{2}\right) \eta \, \left( \xi -1\right) \xi \]\[4 \left( \eta -\frac{1}{2}\right) \eta \, \left( \xi -\frac{1}{2}\right) \xi \]

The shape functions are generated in the tensor product order or lexicographic order, i.e. for the list of support points of these shape functions, their first coordinate component ξ runs faster than the second η.

(%i30)

with_slider_draw3d(i, linspace(1, length(shape_functions_2d), length(shape_functions_2d)), grid=true, enhanced3d=false, color=red, dimensions=fig_size, font=font_name, font_size=fig_font_size,    title=sconcat("Polynomial No.", i),    xlabel="ξ", ylabel="η",    transparent=true,    explicit(shape_functions_2d[i], ξ, 0, 1, η, 0, 1),    color=blue, point_type=filled_circle, point_size=3, enhanced3d=false,    points(makelist([support_points_2d[p,1], support_points_2d[p,2], 0], p, 1, 9)),    points_joined=true, line_type=solid, color=purple, line_width=3, point_size=2,    points([[support_points_2d[i,1], support_points_2d[i,2], 0], [support_points_2d[i,1], support_points_2d[i,2], 1]]) );

2 Map from reference cell to real cell

2.1 1D

A 1D real cell is a line segment, which is embedded in $\mathbb{R}^3$. When this line segment is straight, the map $\chi_{\tau}$ from $[0,1]$ to this real cell is simple, which is merely a translation and rotation from the reference cell $[0,1]$. When this line segment is bent, the map is not trivial. Since a linear combination of the above Lagrange shape functions can be used to approximate any continuous functions defined on the reference cell, it can also be used to approximate the map $\chi_{\tau}$ for this line segment. Because we are in 3D space, we need three such linear combinations of shape functions to represent $x$, $y$ and $z$ coordinate components respectively.

A Lagrange shape function has the property that it is evaluated to 1 at its own support point and to 0 at the support points of the other shape functions. So to make sure that the map $\chi_{\tau}$ produces points located exactly on the bent real cell that correspond to those support points in the reference cell, for each coordinate component respectively, the coefficient before each shape function in the linear combination should be the coodinate component of the point on the real cell which corresponds to the support point of the current shape function in the reference cell.

Now let's define a parametric cubic curve in 3D space. N.B. This corresponds the manifold description of the geometric entity.

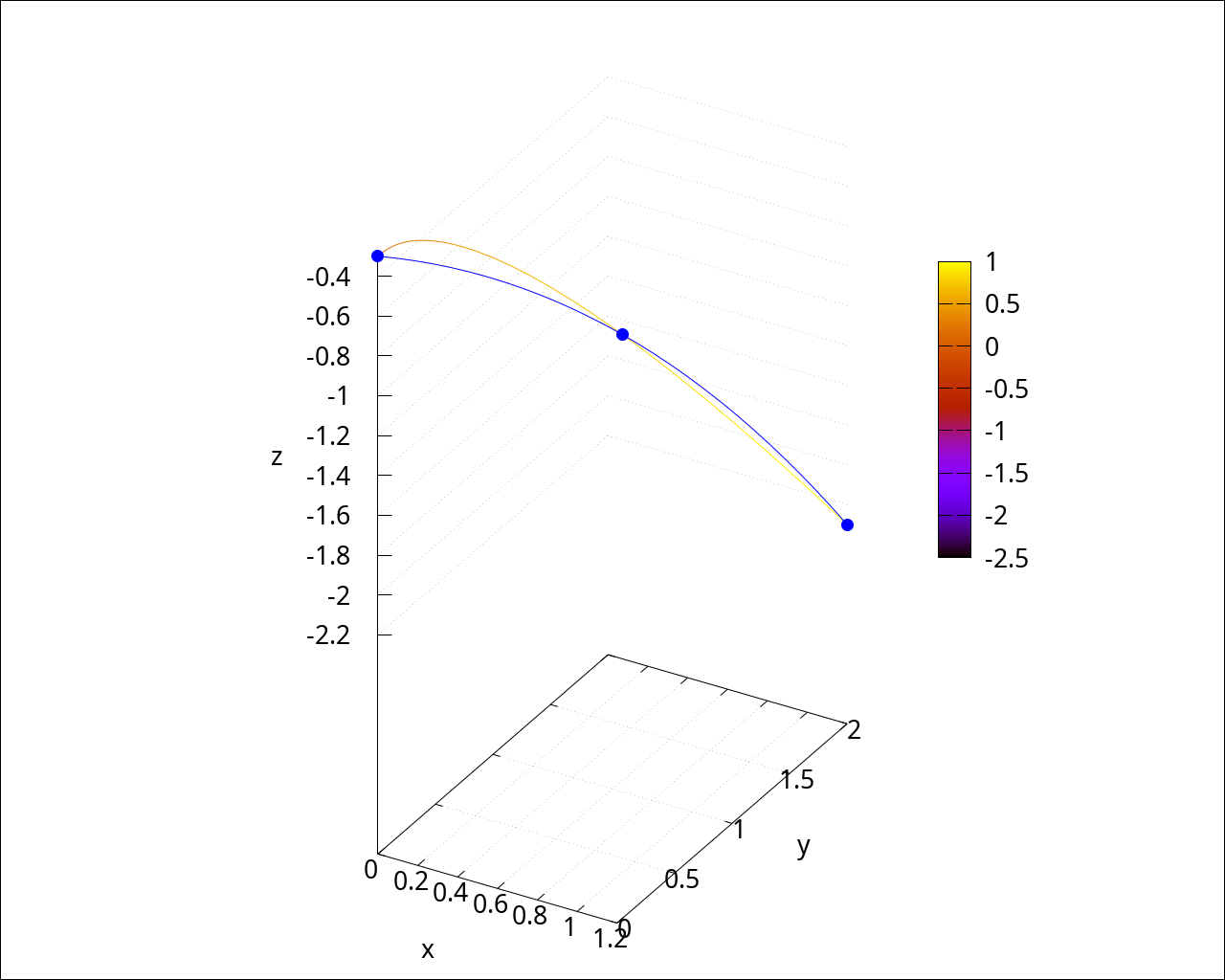
-->	curve(ξ) := [1.2 * ξ^3, 1.5 * ξ^2 + 0.5 * ξ, -2 * ξ^3 - 0.3];

\[\operatorname{ }\operatorname{curve}\left( \xi \right) \operatorname{:=}\left[ 1.2 {{\xi }^{3}}\operatorname{,}1.5 {{\xi }^{2}}+0.5 \xi \operatorname{,}\left( -2\right) {{\xi }^{3}}-0.3\right] \]

The curve looks like this. Here we colorize the curve based on the value of its parameter ξ, which is specified via the option enhanced3d=[ξ, ξ].

-->	wxdraw3d(grid=true, dimensions=fig_size,    terminal=wxt, font=font_name, font_size=fig_font_size, proportional_axes=xyz,    xlabel="x", ylabel="y", zlabel="z",    enhanced3d=[ξ, ξ],    parametric(curve(ξ)[1], curve(ξ)[2], curve(ξ)[3], ξ, 0, 1) );

If we want to use the second order shape functions to represent this curve, besides the two end points, an additional point approximately in the middle of the curve should be provided. This point can be acquired by first taking a convex combination of the two two end points. Then project this new point onto the curve.

Starting and ending points of the curve are

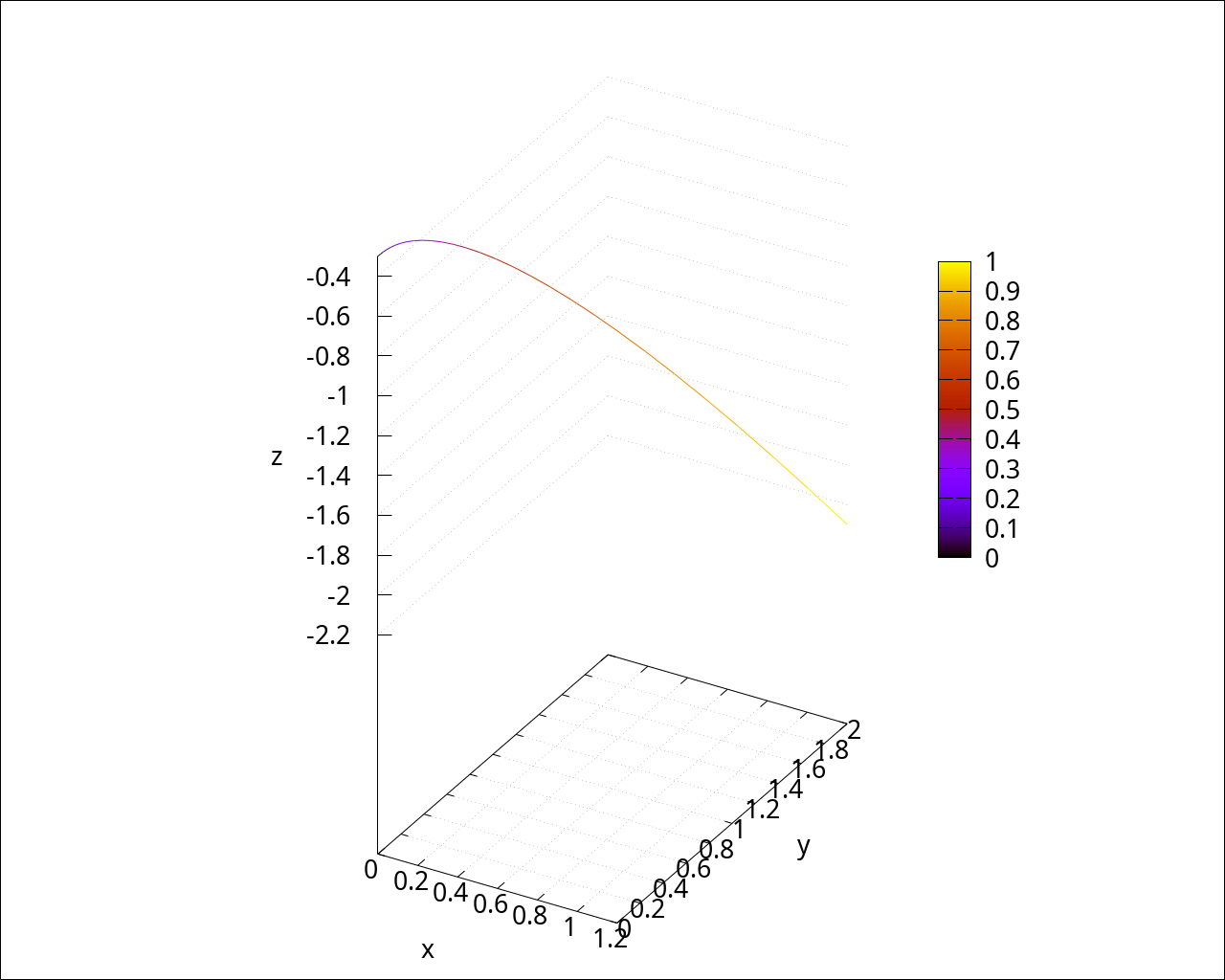
-->	p1 : curve(0); p2 : curve(1);

\[\operatorname{(p1) }\left[ 0\operatorname{,}0\operatorname{,}-0.3\right] \]

\[\operatorname{(p2) }\left[ 1.2\operatorname{,}2.0\operatorname{,}-2.3\right] \]

Convex combination of $p_1$ and $p_2$ is

-->	p_middle : 0.5 * p1 + 0.5 * p2;

\[\operatorname{(p\_ middle) }\left[ 0.6\operatorname{,}1.0\operatorname{,}-1.3\right] \]

Initial guess of the parameter ξ for generating the projection of the middle point on the curve:

-->

ξ0 : 0.5$

Here we let the projection satisfies the condition that the connection line of the above middle point and its projection point is perpendicular to the tangent vector at this projection point. So let's define an objective function which minimizes the dot product of the tangent vector and the connection line.

First, define a function for computing the tangent vector at a point on the curve:

-->	curve_tangent(ξ) := subst(x=ξ, diff(curve(x), x));

\[\operatorname{ }\operatorname{curve\_ tangent}\left( \xi \right) \operatorname{:=}\operatorname{subst}\left( x=\xi \operatorname{,}\frac{d}{d x} \operatorname{curve}(x)\right) \]

Then, the objective function is

-->	project_middle_obj : innerproduct((curve(ξ) - p_middle), curve_tangent(ξ));

\[\]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 3.0 by 3/1 = 3.0 \]\[rat: replaced -1.0 by -1/1 = -1.0 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 1.5 by 3/2 = 1.5 \]\[rat: replaced 0.9999999999999998 by 1/1 = 1.0 \]\[rat: replaced 3.6 by 18/5 = 3.6 \]\[rat: replaced -0.6 by -3/5 = -0.6 \]\[rat: replaced 1.2 by 6/5 = 1.2\]

\[\operatorname{(project\_ middle\_ obj) }\frac{1632 {{\xi }^{5}}+450 {{\xi }^{3}}-591 {{\xi }^{2}}-275 \xi -50}{100}\]

The minimization problem can be solved by the Newton's method.

-->	sol : mnewton([project_middle_obj], [ξ], [ξ0]);

\[\operatorname{(sol) }\left[ \left[ \xi =0.7552127951245737\right] \right] \]

Sustitute this ξ into the curve's parametric equation, we obtain the projection point.

-->	project_middle : curve(rhs(sol[1][1]));

\[\operatorname{(project\_ middle) }\left[ 0.5168794478345868\operatorname{,}1.233125946442094\operatorname{,}-1.161465746390978\right] \]

The support points in the real cell as well as the middle point are shown below. Meanwhile, the support points in the reference cell associated with Lagrange functions are always $[0, 0.5, 1]$. This indicates the curve to be interpolated by Lagrange functions has a different parameterization from its original parametric representation.

-->

wxdraw3d(grid=true, dimensions=fig_size,    terminal=wxt, font=font_name, font_size=fig_font_size, proportional_axes=xyz,    xlabel="x", ylabel="y", zlabel="z",    enhanced3d=[ξ, ξ],    parametric(curve(ξ)[1], curve(ξ)[2], curve(ξ)[3], ξ, 0, 1),    color=red, point_type=circle, point_size=2, enhanced3d=false,    points([p_middle]),    color=blue, point_type=filled_circle, point_size=3, enhanced3d=false,    points([p1, project_middle, p2]),    color=blue, point_type=-1, enhanced3d=false, points_joined=true, line_type=dashes,    points([p1, p2]),    color=blue, point_type=-1, enhanced3d=false, points_joined=true, line_type=dashes,    points([p_middle, project_middle]) );

Then the map from the reference cell to the real cell can be constructed using 2nd order 1D Lagrange shape functions.

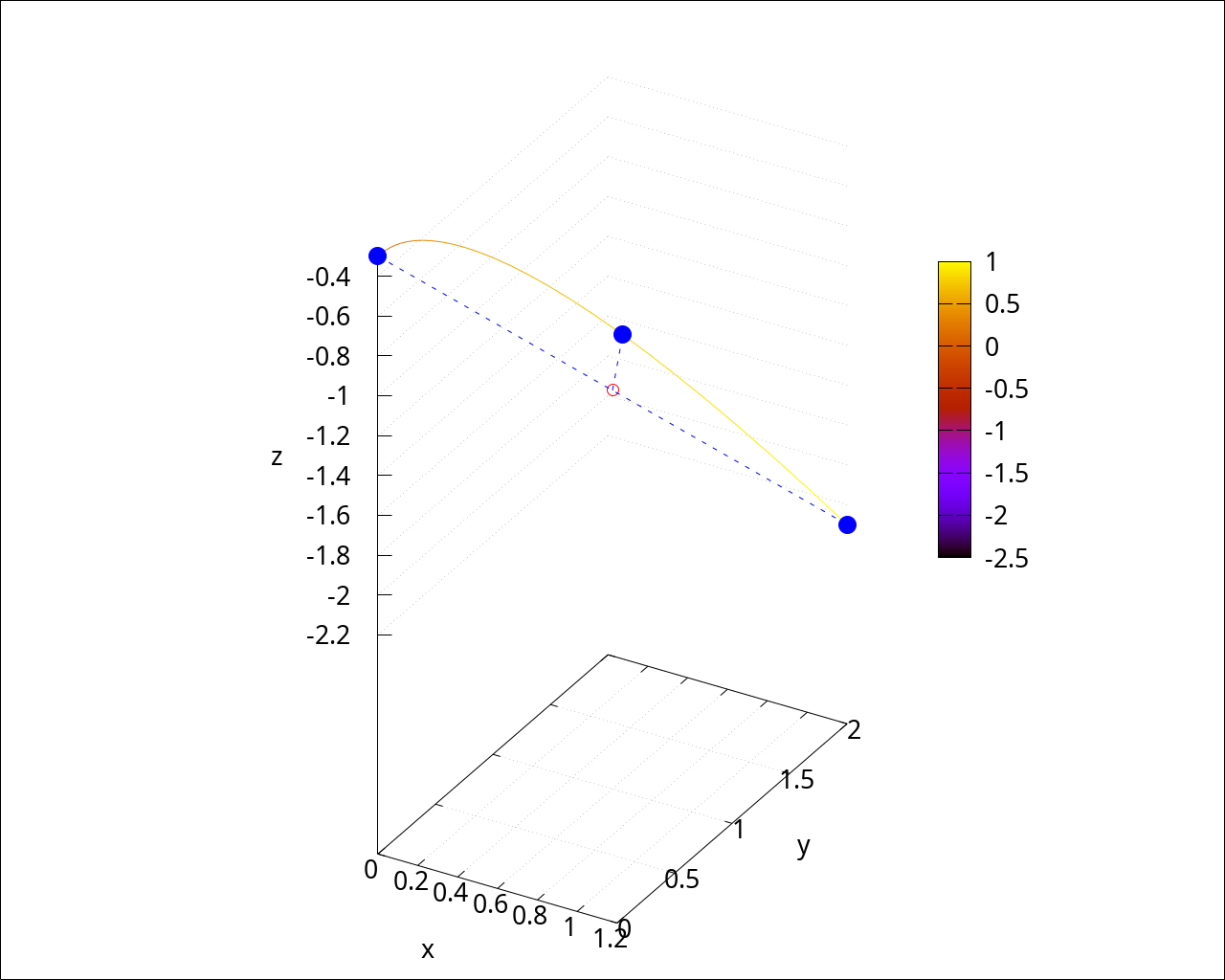
-->	shape_functions_1d : GenLagrangeBases1D(2, reference_cell_1d, 'ξ);

\[\operatorname{(shape\_ functions\_ 1d) }\left[ 2 \left( \xi -1\right) \, \left( \xi -\frac{1}{2}\right) \operatorname{,}-4 \left( \xi -1\right) \xi \operatorname{,}2 \left( \xi -\frac{1}{2}\right) \xi \right] \]

-->	map_from_ref_to_real_1d : p1 * shape_functions_1d[1] + project_middle * shape_functions_1d[2] + p2 * shape_functions_1d[3]$ PrintEquationList(map_from_ref_to_real_1d);

\[\]\[2.4 \left( \xi -\frac{1}{2}\right) \xi -2.067517791338348 \left( \xi -1\right) \xi \]\[4.0 \left( \xi -\frac{1}{2}\right) \xi -4.932503785768375 \left( \xi -1\right) \xi \]\[-4.6 \left( \xi -\frac{1}{2}\right) \xi +4.645862985563912 \left( \xi -1\right) \xi -0.6 \left( \xi -1\right) \, \left( \xi -\frac{1}{2}\right) \]

Now we plot the interpolated curve using 2nd order Lagrange functions together with the original curve. We can see that the interpolated curve exactly passes through the three support points in the real cell.

-->

wxdraw3d(grid=true, dimensions=fig_size,    terminal=wxt, font=font_name, font_size=fig_font_size, proportional_axes=xyz,    xlabel="x", ylabel="y", zlabel="z",    enhanced3d=[ξ, ξ],    parametric(curve(ξ)[1], curve(ξ)[2], curve(ξ)[3], ξ, 0, 1),    color=blue, enhanced3d=false,    parametric(map_from_ref_to_real_1d[1], map_from_ref_to_real_1d[2], map_from_ref_to_real_1d[3], ξ, 0, 1),    color=blue, point_type=filled_circle, point_size=2, enhanced3d=false,    points([p1, project_middle, p2]) );

2.2 2D

Similarto the 1D case, a 2D real cell embedded in $\mathbb{R}^3$ is an arbitrary quadrilateral, either flat or curved and not necessarily a parallelogram. Therefore, the map $\chi_{\tau}$ from the 2D reference cell $[0,1] \times [0,1]$ to a real cell can be expanded by a set of 2D Lagrange shape functions. When the Lagrange polynomial order is 1, the mapped real cell is planar. When the order is higher than 1, the mapped real cell is curved. Such a map is actually a linear combination of the shape functions weighted by corresponding support point coordinates. The basic philosophy of computing the projection of intermediate points which are to be used as support points of shape functions is similar and no examples are given here.

3 Basis functions of finite element

The shape functions adopted by a discontinuous finite element, which conforms to the $L^2$ function space, can use Lagrange polynomials defined on the reference cell $[0,1] \times [0,1]$. Hence, the shape functions in each cell in the domain on which the finite element is defined corresponds to a unique basis function of the finite element space.

Even though the continuous finite element adtops the same shape functions as the discontinuous finite element, because it conforms to the Sobolev space $H^1$, functions constructed from this finite element should be continuous across cell boundaries. Then for a basis function in the finite element space, when its support point is in the interior of a cell, the situation is simple and it is just the shape function with the same support point in this cell. When the support point of the basis function in on an edge, face or a vertex, such support point will be shared by several cells. Then the basis function of the finite element space determined by the continuous finite element is a concatenation of those shape functions in these cells whose support points are just the common support point of the basis function.

Let's use the sphere model as an example.

Figure 1:Mesh for a sphere

We select four cells from the mesh and construct the basis function situated at node #8 in the continuous finite element space.

Figure 2:Four elements from the mesh for the sphere

The vertices in each cell are enumerated below.
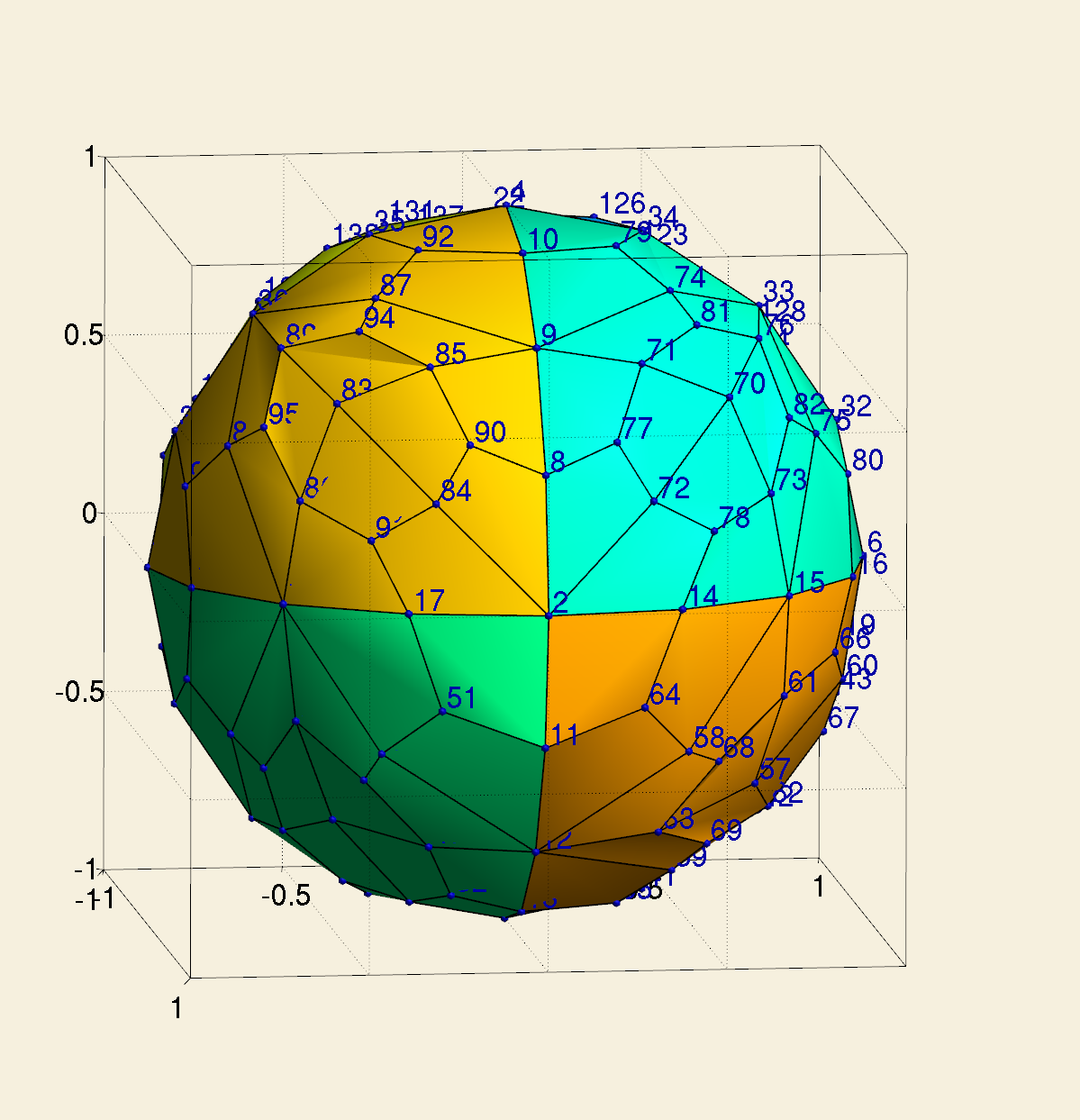
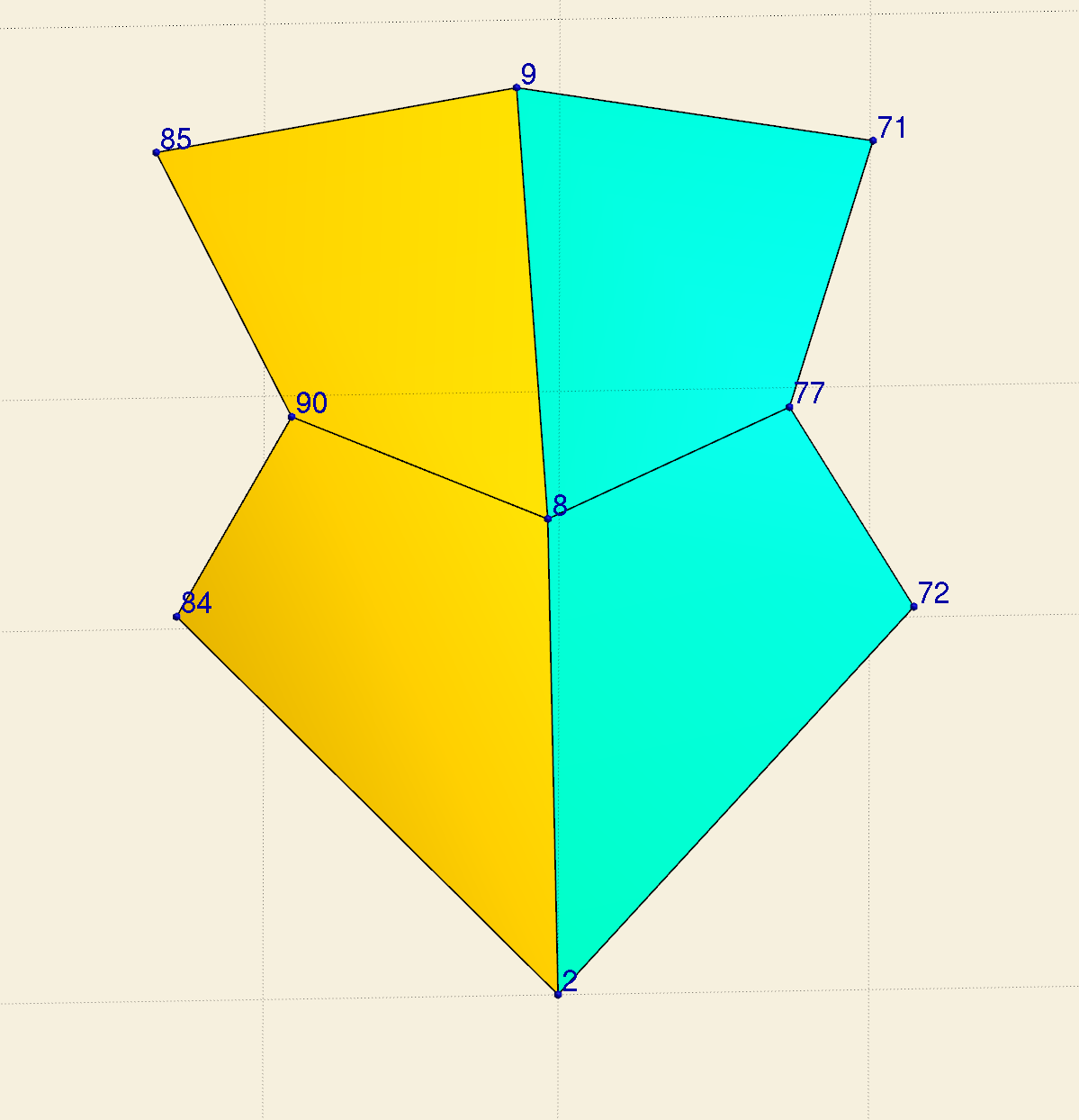
Cell 92: [9 71 77 8]
Cell 94: [8 77 72 2]
Cell 110: [2 84 90 8]
Cell 112: [8 90 85 9]

These vertices are arranged in the clockwise order. When the mesh is read into a FEM solver, these vertices will be rearranged into lexicographic order for example by swapping the last two vertices in a cell. Hence they become
Cell 92: [9 71 8 77]
Cell 94: [8 77 2 72]
Cell 110: [2 84 8 90]
Cell 112: [8 90 9 85]

Then shape functions with indices [1,2,3,4] defined by a first order continuous finite element in the reference cell will be assigned to these vertices in order. Therefore, for the basis function at node #8 in the finite element space, it is a concatenation of 4 shape functions:
Shape function #3 in the reference cell corresponding to cell 92
Shape function #1 in the reference cell corresponding to cell 94
Shape function #3 in the reference cell corresponding to cell 110
Shape function #1 in the reference cell corresponding to cell 112

To visualize the distribution of basis function on these four cells, which are actually its support set, we can plot four parametric surfaces using the map from each reference cell to its corresponding real cell. Then, we colorize the parametric surface using the value of related shape function.

Vertex coordinates

-->	node9 : [0, 0.7071067827963321, 0.7071067795767629]$

-->	node71 : [0.2959042210220728, 0.6562956747206669, 0.6940581238803165]$

-->	node77 : [0.2069290967160619, 0.4625779322341045, 0.8620916456748057]$

-->	node8 : [0, 0.382683433164956, 0.9238795321799713]$

-->	node72 : [0.3048963989653106, 0.3017651820890481, 0.903313877219181]$

-->	node2 : [0, 0, 1]$

-->	node84 : [-0.3037257264799272, 0.3035840488652949, 0.9030987810581932]$

-->	node90 : [-0.2041682670359604, 0.461491589969017, 0.8633312406738223]$

-->	node85 : [-0.2959042210220861, 0.6562956747206589, 0.6940581238803184]$

Because the cells are flat, we use first order shape function in the map from reference cell to real cells.

-->	shape_functions_for_map_2d : GenLagrangeBases2D([1, 1], reference_cell_1d, reference_cell_1d, '[ξ, η]);

\[\operatorname{(shape\_ functions\_ for\_ map\_ 2d) }\left[ \left( 1-\eta \right) \, \left( 1-\xi \right) \operatorname{,}\left( 1-\eta \right) \xi \operatorname{,}\eta \, \left( 1-\xi \right) \operatorname{,}\eta \xi \right] \]

-->	cell92_map : node9 * shape_functions_for_map_2d[1] + node71 * shape_functions_for_map_2d[2] + node8 * shape_functions_for_map_2d[3] + node77 * shape_functions_for_map_2d[4]$

-->	cell94_map : node8 * shape_functions_for_map_2d[1] + node77 * shape_functions_for_map_2d[2] + node2 * shape_functions_for_map_2d[3] + node72 * shape_functions_for_map_2d[4]$

-->	cell110_map : node2 * shape_functions_for_map_2d[1] + node84 * shape_functions_for_map_2d[2] + node8 * shape_functions_for_map_2d[3] + node90 * shape_functions_for_map_2d[4]$

-->	cell112_map : node8 * shape_functions_for_map_2d[1] + node90 * shape_functions_for_map_2d[2] + node9 * shape_functions_for_map_2d[3] + node85 * shape_functions_for_map_2d[4]$

When the continuous finite element space is first order, its shape functions are the same as the shape functions used by the first order map.

-->	shape_functions_for_finite_element : shape_functions_for_map_2d$

-->

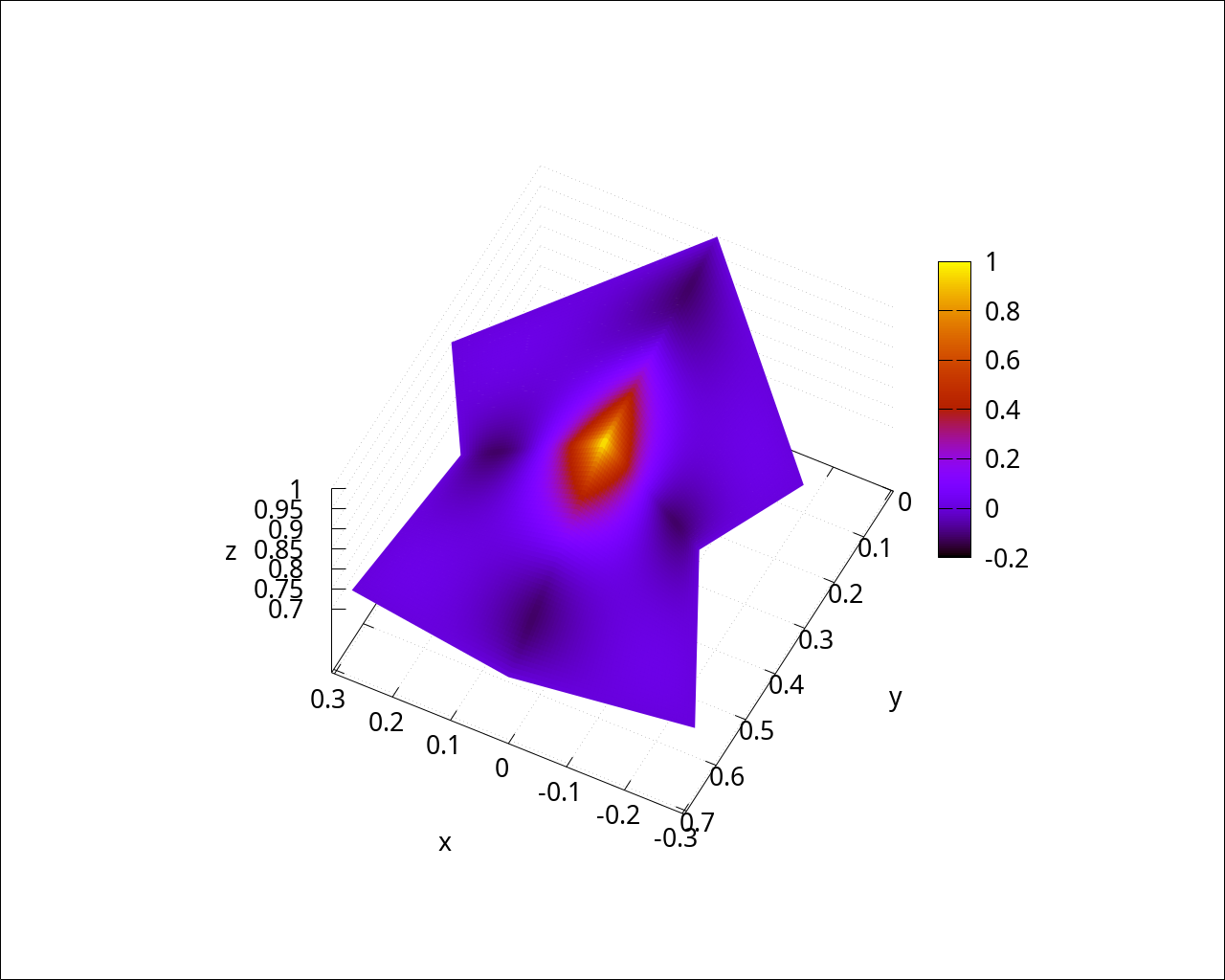
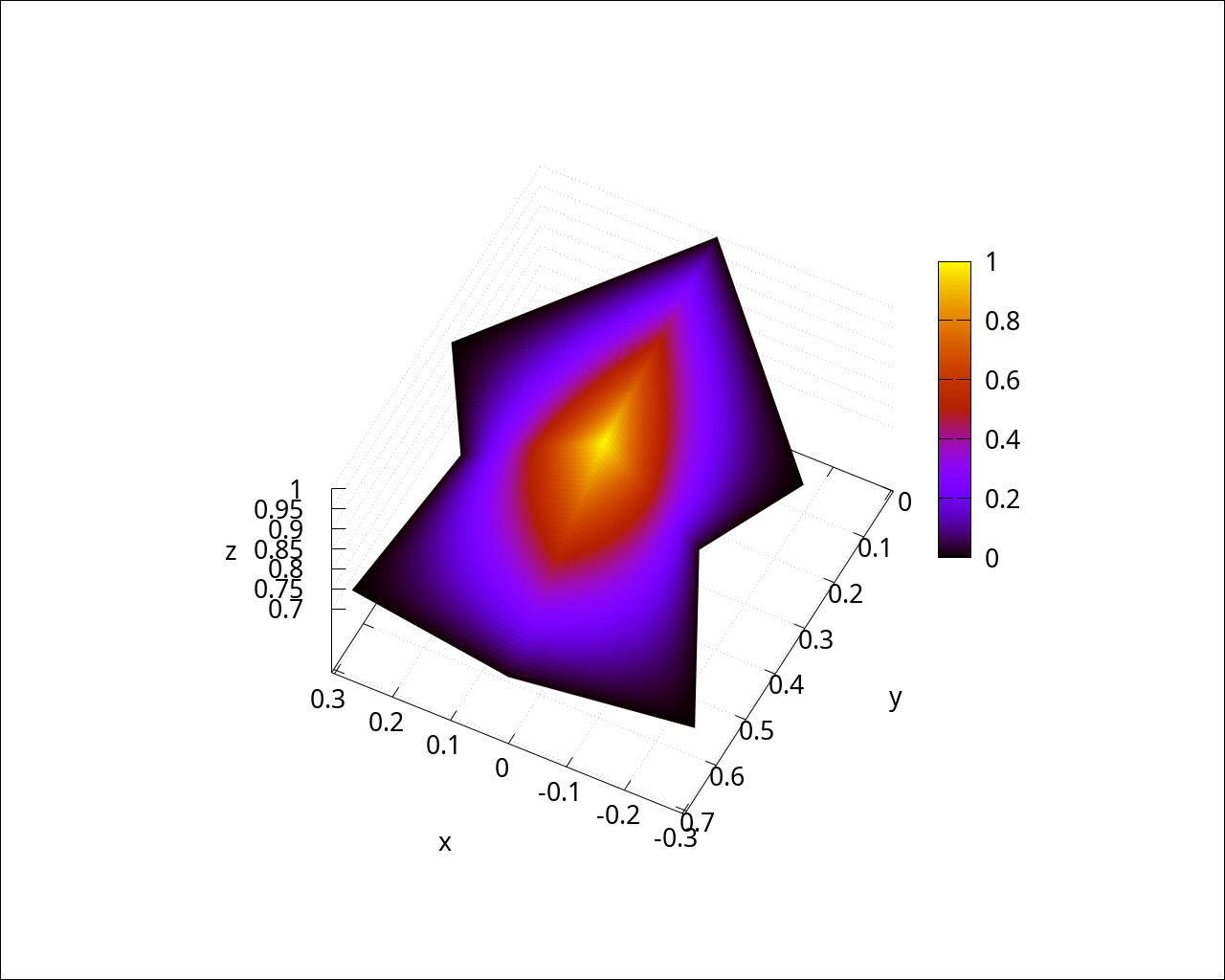
wxdraw3d(grid=true, dimensions=fig_size,    terminal=wxt, font=font_name, font_size=fig_font_size, proportional_axes=xyz,    xlabel="x", ylabel="y", zlabel="z", view=[38,207],    enhanced3d=[shape_functions_for_finite_element[3], ξ, η],    parametric_surface(cell92_map[1], cell92_map[2], cell92_map[3], ξ, 0, 1, η, 0, 1),    enhanced3d=[shape_functions_for_finite_element[1], ξ, η],    parametric_surface(cell94_map[1], cell94_map[2], cell94_map[3], ξ, 0, 1, η, 0, 1),    enhanced3d=[shape_functions_for_finite_element[3], ξ, η],    parametric_surface(cell110_map[1], cell110_map[2], cell110_map[3], ξ, 0, 1, η, 0, 1),    enhanced3d=[shape_functions_for_finite_element[1], ξ, η],    parametric_surface(cell112_map[1], cell112_map[2], cell112_map[3], ξ, 0, 1, η, 0, 1)    );

If the finite element is 2nd order continuous, the shape functions in the reference cell are organized in the lexicographic order:
^
| 7 8 9
| 4 5 6
| 1 2 3
---------->

Then for the basis function at node #8 in the finite element space, it is a concatenation of 4 shape functions:
Shape function #7 in the reference cell corresponding to cell 92
Shape function #1 in the reference cell corresponding to cell 94
Shape function #7 in the reference cell corresponding to cell 110
Shape function #1 in the reference cell corresponding to cell 112

Define Lagrange shape functions for the 2nd order finite element:

-->	shape_functions_for_finite_element : GenLagrangeBases2D([2, 2], reference_cell_1d, reference_cell_1d, '[ξ, η])$ PrintEquationList(shape_functions_for_finite_element);

\[\]\[4 \left( \eta -1\right) \, \left( \eta -\frac{1}{2}\right) \, \left( \xi -1\right) \, \left( \xi -\frac{1}{2}\right) \]\[-8 \left( \eta -1\right) \, \left( \eta -\frac{1}{2}\right) \, \left( \xi -1\right) \xi \]\[4 \left( \eta -1\right) \, \left( \eta -\frac{1}{2}\right) \, \left( \xi -\frac{1}{2}\right) \xi \]\[-8 \left( \eta -1\right) \eta \, \left( \xi -1\right) \, \left( \xi -\frac{1}{2}\right) \]\[16 \left( \eta -1\right) \eta \, \left( \xi -1\right) \xi \]\[-8 \left( \eta -1\right) \eta \, \left( \xi -\frac{1}{2}\right) \xi \]\[4 \left( \eta -\frac{1}{2}\right) \eta \, \left( \xi -1\right) \, \left( \xi -\frac{1}{2}\right) \]\[-8 \left( \eta -\frac{1}{2}\right) \eta \, \left( \xi -1\right) \xi \]\[4 \left( \eta -\frac{1}{2}\right) \eta \, \left( \xi -\frac{1}{2}\right) \xi \]

The basis function at node #8 can be plotted as below.

-->

wxdraw3d(grid=true, dimensions=fig_size,    terminal=wxt, font=font_name, font_size=fig_font_size, proportional_axes=xyz,    xlabel="x", ylabel="y", zlabel="z", view=[38,207],    enhanced3d=[shape_functions_for_finite_element[7], ξ, η],    parametric_surface(cell92_map[1], cell92_map[2], cell92_map[3], ξ, 0, 1, η, 0, 1),    enhanced3d=[shape_functions_for_finite_element[1], ξ, η],    parametric_surface(cell94_map[1], cell94_map[2], cell94_map[3], ξ, 0, 1, η, 0, 1),    enhanced3d=[shape_functions_for_finite_element[7], ξ, η],    parametric_surface(cell110_map[1], cell110_map[2], cell110_map[3], ξ, 0, 1, η, 0, 1),    enhanced3d=[shape_functions_for_finite_element[1], ξ, η],    parametric_surface(cell112_map[1], cell112_map[2], cell112_map[3], ξ, 0, 1, η, 0, 1)    );