Summary of Green's identities
Contents
2 Representation formula for the Laplace equation: the third Green’s identity
3 General formulation of Green’s identities
Green’s identities are indispensable for solving partial differential equations. For example, consider the Poisson’s equation \begin{equation} -\Delta u = f \quad \text {in \(\Omega \)}, \end{equation} with a Dirichlet boundary condition \(\gamma _0 u=g_{\mathrm {D}}\) on \(\Gamma _{\mathrm {D}}\) and Neumann condition \(\gamma _1u = g_{\mathrm {N}}\) on \(\Gamma _{\mathrm {N}}\). We can apply a test function \(v\in H_0^1(\Omega )\) to both sides of the equation: \begin{equation} \int _{\Omega } -v\Delta u \intd x = \int _{\Omega } fv \intd x. \end{equation} Then use the Green’s first identity \begin{equation} \int _{\Omega }v\Delta u \intd x =-\int _{\Omega } (\nabla u)\cdot (\nabla v) \intd x + \int _{\pdiff \Omega } v \frac {\pdiff u}{\pdiff \vect {n}} \intd s, \end{equation} and consider the fact that \(v\) vanishes on \(\Gamma _{\mathrm {D}}\), we have the weak form or variational form of the original equation as \begin{equation} \int _{\Omega } (\nabla u)\cdot (\nabla v) \intd x = -\int _{\Omega }v\Delta u \intd x + \int _{\pdiff \Omega } v \frac {\pdiff u}{\pdiff \vect {n}} \intd s = -\int _{\Omega } fv \intd x + \int _{\Gamma _{\mathrm {N}}} v \frac {\pdiff u}{\pdiff \vect {n}} \intd s. \end{equation} This equation can be directly solved using the FEM.
If the BEM is used, the procedure is to first represent the solution \(u\) in the domain \(\Omega \) using an integral form, then take the limit \(x \rightarrow \Gamma \) , i.e. let the target point approach the domain boundary, and a boundary integral equation (BIE) can be obtained using the limiting properties of integral operators. The derivation of the representation formula also involves the second Green’s identity.
Therefore, in this essay, I will summarize various forms of Green’s identities.
1 Classical formulation of Green’s identities
Theorem 1 (Gauss-Ostrogradski Theorem) Let \(u\in C^1(\bar \Omega )\). Then \begin{equation} \int _{\Omega } \frac {\pdiff u}{\pdiff x_{i}} \intd x = \int _{\pdiff \Omega } \gamma _0^{\rm int}u n_i \intd s \quad i=1,\cdots ,d, \end{equation} where \(n_i\) is the \(i\)-th component of the outward unit normal vector field at \(x\), \(\gamma _0^{\rm int}\) is the Dirichlet trace operator.
Proof Assume the \(d\) dimensional domain \(\Omega \) is convex. Then the value range, i.e. lower bound and upper bound, for the \(i\)-th coordinate \(x_i\) can be represented by the other coordinate components as \begin{equation} x_i \in [f_{\mathrm {L}}(x_1,\cdots ,\hat {x_i},\cdots ,x_d), f_{\mathrm {H}}(x_1,\cdots ,\hat {x_i},\cdots ,x_d)]. \end{equation} The two equations \begin{equation} \label {eq:lower-bound-xi-domain-boundary} x_i = f_{\mathrm {L}}(x_1,\cdots ,\hat {x_i},\cdots ,x_d) \end{equation} and \begin{equation} \label {eq:upper-bound-xi-domain-boundary} x_i = f_{\mathrm {H}}(x_1,\cdots ,\hat {x_i},\cdots ,x_d) \end{equation} determine two subsets of the boundary \(\partial \Omega \), which are \(d-1\) dimensional manifolds in \(\mathbb {R}^d\).
Using the Fubini’s theorem, the left hand side integration on \(\Omega \) can be split into to two successive parts, one is with respect to the coordinate \(x_i\), the other is with respect to remaining coordinates: \begin{equation} \int _{\Omega } \frac {\pdiff u}{\pdiff x_i} \intd x = \int _U \intd x_1\cdots \intd \hat {x_i}\cdots \intd x_d \int _{f_{\mathrm {L}}(x_1,\cdots ,\hat {x_i},\cdots ,x_d)}^{f_{\mathrm {H}}(x_1,\cdots ,\hat {x_i},\cdots ,x_d)} \frac {\pdiff u}{\pdiff x_i} \intd x_i, \end{equation} where \(U\) is the integration domain with respect to the remaining coordinate variables. Therefore, the left hand side of the Gauss-Ostrogradski identity is equal to \begin{equation} \int _U \left [ u(x_1,\cdots ,f_{\mathrm {H}},\cdots ,x_d) - u(x_1,\cdots ,f_{\mathrm {L}},\cdots ,x_d) \right ] \intd x_1\cdots \intd \hat {x_i}\cdots \intd x_d. \end{equation}
For \(n^i\) in the boundary integral on the right hand side, it is the \(i\)-th component of the outward normal vector of \(\partial \Omega \). Because Equation (7) describes the lower domain boundary with respect to the \(i\)-th coordinate (written as \(\partial \Omega _{\mathrm {L}_i}\)) and Equation (8) describes the upper domain boundary \(\partial \Omega _{\mathrm {H}_i}\), \(n^i < 0\) on \(\partial \Omega _{\mathrm {L}_i}\) and \(n^i > 0\) on \(\partial \Omega _{\mathrm {H}_i}\). For remaining parts of \(\partial \Omega \), \(n^i=0\). This is illustrated in the following figure.
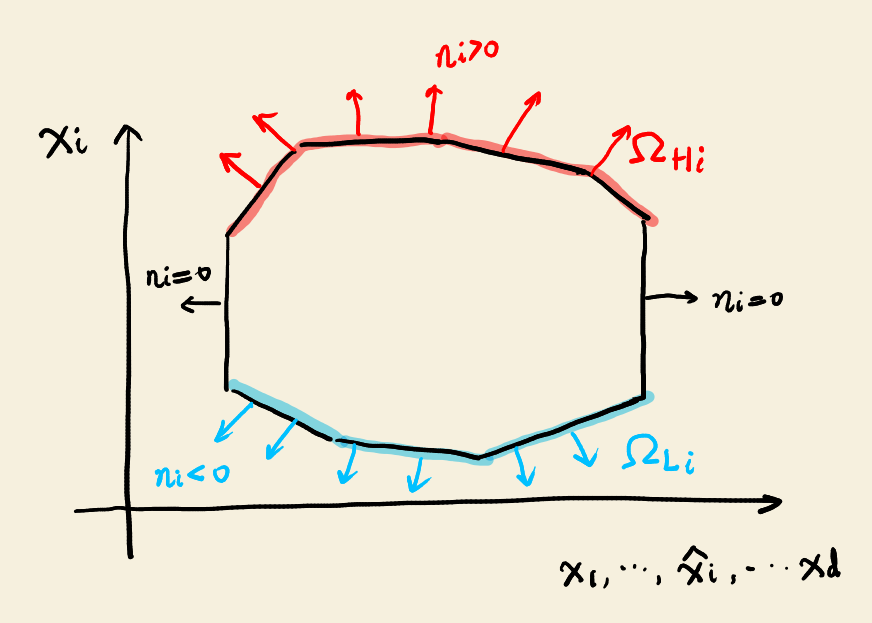
Furthermore, because the geometric meaning of \(n^{i}\) is the cosine of the angle between the outward normal vector and the \(i\)-th coordinate axis, \(n^i \intd s\) is actually a signed projection of the surface integral element \(\intd s\) to the multi-dimensional coordinate “plane” spanned by \((x_1,\cdots ,\hat {x_i},\cdots ,x_d)\).
Therefore, the right hand side is \begin{equation} \begin {aligned} \rhs &= \int _{\partial \Omega _{\mathrm {H}_i}} u(x_1,\cdots ,f_{\mathrm {H}},\cdots ,x_d) n^i \intd s + \int _{\partial \Omega _{\mathrm {L}_i}} u(x_1,\cdots ,f_{\mathrm {L}},\cdots ,x_d) n^i \intd s \\ &= \int _U \left [ u(x_1,\cdots ,f_{\mathrm {H}},\cdots ,x_d) - u(x_1,\cdots ,f_{\mathrm {L}},\cdots ,x_d) \right ] \intd x_1\cdots \intd \hat {x_i}\cdots \intd x_d \end {aligned}. \end{equation} This is just the same as the left hand side.
When the domain is not convex, we can split it into several convex subdomains \(\left \{\Omega \right \}_{i=1}^n\) and apply the above conclusion to each \(\Omega _i\). Then we add the identities for all subdomains. Because the boundary integrals cancel on interior interfaces, the sum of these identities is the Gauss-Ostrogradski identity for the global domain \(\Omega \).
Theorem 2 (Gauss divergence Theorem) Let \(u\in \left [ C^1(\bar \Omega ) \right ]^d\). Then \begin{equation} \int _{\Omega } \divergence \vect {u} \intd x = \int _{\pdiff \Omega } \gamma _0^{\rm int} \vect {u}\cdot \vect {n} \intd s. \end{equation}
Proof Apply the Gauss-Ostrogradski Theorem 1 to each term in \(\divergence \vect {u}\).
Theorem 3 (Integration by parts) Let \(u,v\in C^1(\bar \Omega )\). Then \begin{equation} \int _{\Omega }\frac {\pdiff u}{\pdiff x_i} v \intd x + \int _{\Omega } u \frac {\pdiff v}{\pdiff x_i} \intd x = \int _{\pdiff \Omega } \left ( \gamma _0^{\rm int}u \right ) \left ( \gamma _0^{\rm int}v \right ) n_i \intd s. \end{equation}
Proof Apply the Gauss-Ostrogradski Theorem 1 to \(uv\).
Proposition 1 Let \(u\in C^2(\bar \Omega )\). \begin{equation} \int _{\Omega } \Delta u \intd x = \int _{\pdiff \Omega } \frac {\pdiff u}{\pdiff \vect {n}} \intd s. \end{equation}
Proof Apply Gauss divergence Theorem 2 to \(\nabla u\) or replace \(u\) with \(\frac {\pdiff u}{\pdiff x_{i}}\) and \(v\) with \(1\) in Theorem 3.
Theorem 4 (Green’s first identity) Let \(u,v\in C^2(\bar \Omega )\). \begin{equation} \label {eq:green-1st-identity} \begin {aligned} \int _{\Omega }v\Delta u \intd x &=-\int _{\Omega } (\nabla u)\cdot (\nabla v) \intd x + \int _{\pdiff \Omega } v \frac {\pdiff u}{\pdiff \vect {n}} \intd s \\ \int _{\Omega }u\Delta v \intd x &=-\int _{\Omega } (\nabla u)\cdot (\nabla v) \intd x + \int _{\pdiff \Omega } u \frac {\pdiff v}{\pdiff \vect {n}} \intd s \end {aligned}. \end{equation}
Proof To prove the first equation, replace \(u\) with \(\frac {\pdiff u}{\pdiff x_{i}}\) in Theorem 3, we have \[ \int _{\Omega }\frac {\pdiff ^2 u}{\pdiff x_i^2} v \intd x=\int _{\pdiff \Omega } \frac {\pdiff u}{\pdiff x_i} v n_i \intd s - \int _{\Omega }\frac {\pdiff u}{\pdiff x_i}\frac {\pdiff v}{\pdiff x_{i}} \intd x. \] Then sum up this relation for \(i=1,\cdots ,d\) and the first equation is obtained. The proof of the second equation is similar.
Theorem 5 (Green’s second identity) Let \(u,v\in C^2(\bar \Omega )\). \begin{equation} \label {eq:green-2nd-identity} \int _{\Omega } \left ( v\Delta u - u\Delta v \right ) \intd x = \int _{\pdiff \Omega } \left [ v \frac {\pdiff u}{\pdiff \vect {n}} - u \frac {\pdiff v}{\pdiff \vect {n}} \right ] \intd s. \end{equation}
Proof Subtract the two equations in Theorem 4, we get the Green’s second identity.
2 Representation formula for the Laplace equation: the third Green’s identity
Consider the Green’s second identity (16), we replace \(v\) with the fundamental solution \(U^{\ast }(x,y)=\frac {1}{\lvert x-y \rvert }\) of the Laplace equation and \(u\) with a harmonic function \(\varphi (y)\): \begin{equation} \int _{\Omega } \left ( U^{\ast }(x,y)\Delta _y \varphi - \varphi \Delta _y U^{\ast }(x,y) \right ) \intd y = \int _{\pdiff \Omega } \left [ U^{\ast }(x,y) \frac {\pdiff \varphi }{\pdiff \vect {n}_y} - \varphi \frac {\pdiff U^{\ast }(x,y)}{\pdiff \vect {n}_y} \right ] \intd s_y, \end{equation} where \(x\in \Omega \). Because \(\varphi \) is harmonic, the first term on the left hand side is zero. The singularity in the second integral on the left hand side should be evaluated in the sense of Cauchy principal value, i.e. we remove a ball \(B_{\varepsilon }(x)\) with a radius \(\varepsilon \) around the singularity \(x\) from \(\Omega \), then apply the second Green’s identity in \(\tilde {\Omega }:= \Omega \backslash B_{\varepsilon }(x)\), and finally take the limit \(\varepsilon \rightarrow 0\).
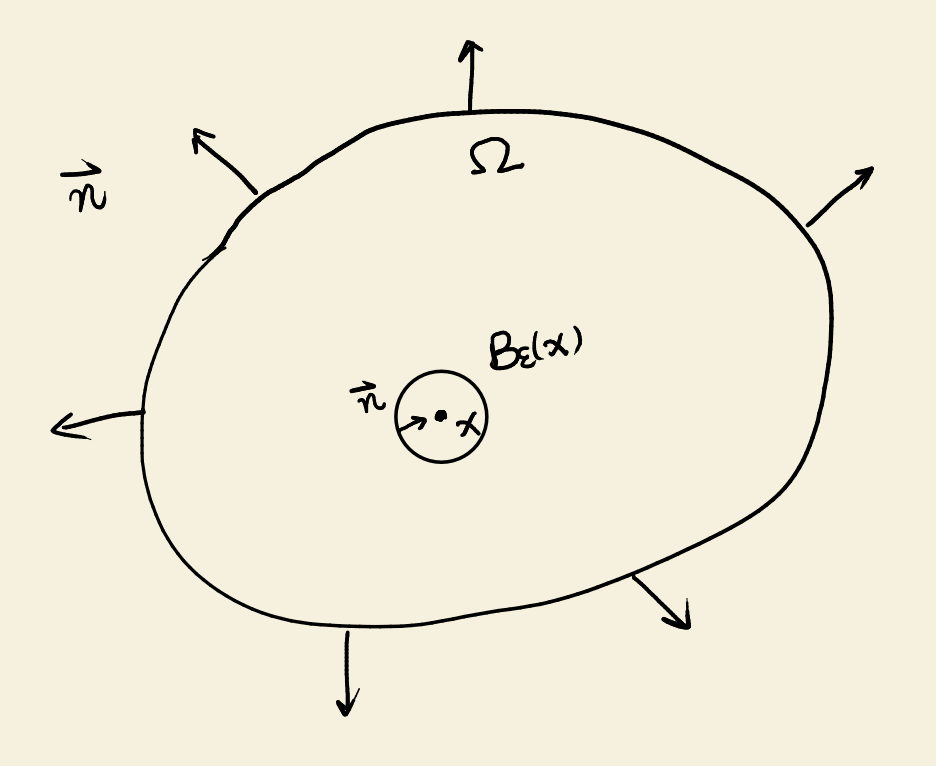
The left hand side is \begin{equation} -\int _{\tilde {\Omega }} \varphi \Delta _y U^{\ast }(x,y) \intd y. \end{equation} The fundamental solution \(U^{\ast }(x-y)\) is singular at \(x\) and harmonic elsewhere, so it is always zero in \(\tilde {\Omega }\). When \(\varepsilon \rightarrow 0\), the left hand side is zero.
Because the boundary of \(\tilde {\Omega }\) comprises two parts \(\partial \Omega \) and \(\partial B_{\varepsilon }(x)\), the right hand side is \begin{equation} \int _{\partial \Omega } \left [ U^{\ast }(x,y) \frac {\pdiff \varphi }{\pdiff \vect {n}_y} - \varphi \frac {\pdiff U^{\ast }(x,y)}{\pdiff \vect {n}_y} \right ] \intd s_y + \int _{\partial B_{\varepsilon }(x)} \left [ U^{\ast }(x,y) \frac {\pdiff \varphi }{\pdiff \vect {n}_y} - \varphi \frac {\pdiff U^{\ast }(x,y)}{\pdiff \vect {n}_y} \right ] \intd s_y. \end{equation} Because \(x\in \Omega \) and \(y\in \partial \Omega \), the first term has no singularity and we just keep it there.
In the second term, the normal vector \(\vect {n}_y\) at \(\partial B_{\varepsilon }(x)\) points inward and is equal to \(\frac {x-y}{\lvert x-y \rvert }\). The normal derivative of the harmonic function is \begin{equation} \frac {\partial \varphi }{\partial \vect {n}_y} = \nabla \varphi \cdot \frac {x-y}{\lvert x-y \rvert }. \end{equation} Then \begin{equation} U^{\ast }(x,y)\frac {\partial \varphi }{\partial \vect {n}_y} = \frac {1}{4\pi \lvert x-y \rvert } \nabla \varphi \cdot \frac {x-y}{\lvert x-y \rvert } = \frac {1}{4\pi \varepsilon } \nabla \varphi \cdot \frac {x-y}{\lvert x-y \rvert }. \end{equation} When \(\varphi \in C^2(\Omega )\), \(\nabla \varphi \) is a continuous vector field. When \(\varepsilon \) is small enough, \(\nabla \varphi \) is nearly a constant vector field through \(B_{\varepsilon }(x)\). Therefore, its flux at antipodal points on \(\partial B_{\varepsilon }(x)\) cancel out.
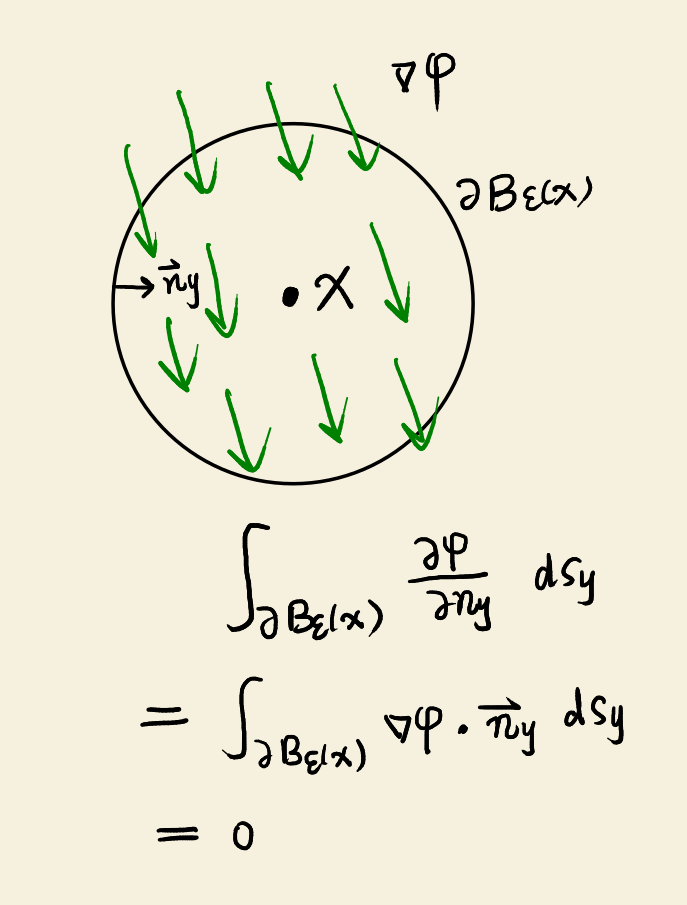
Therefore, when \(\varepsilon \rightarrow 0\), \begin{equation} \int _{\partial B_{\varepsilon }(x)} U^{\ast }(x,y)\frac {\partial \varphi }{\partial \vect {n}_y} \intd s_y = \frac {1}{4\pi \varepsilon } \int _{\partial B_{\varepsilon }(x)} \nabla \varphi \cdot \frac {x-y}{\lvert x-y \rvert } \intd s_y = 0. \end{equation}
The normal derivative of the fundamental solution is \begin{equation} \frac {\partial U^{\ast }(x,y)}{\partial \vect {n}_y} = \nabla _y U^{\ast }(x,y) \cdot \vect {n}_y = \nabla _y U^{\ast }(x,y) \cdot \frac {x-y}{\lvert x-y \rvert } = \frac {x-y}{4\pi \lvert x-y \rvert ^3} \frac {x-y}{\lvert x-y \rvert } = \frac {1}{4\pi \lvert x-y \rvert ^2}. \end{equation} Because \(\lvert x-y \rvert = \varepsilon \), \begin{equation} \int _{\partial B_{\varepsilon }(x)} - \varphi (y) \frac {1}{4\pi \varepsilon ^2} \intd s_y. \end{equation} When \(\varepsilon \rightarrow 0\), \(\varphi (y) \rightarrow \varphi (x)\) and the above integral is just \(-\varphi (x)\).
Summarizing above results, we have the representation formula \begin{equation} \varphi (x) = \int _{\partial \Omega } \left [ U^{\ast }(x,y) \frac {\pdiff \varphi }{\pdiff \vect {n}_y} - \varphi \frac {\pdiff U^{\ast }(x,y)}{\pdiff \vect {n}_y} \right ] \intd s_y \quad x\in \Omega , \end{equation} which is a combination of single layer potential and double layer potential. Such a representation formula is also called the third Green’s identity.
3 General formulation of Green’s identities
Let \(X\) be a Hilbert space with the inner product \(\left \langle \cdot ,\cdot \right \rangle _X\) and the induced norm \(\sqrt {\left \langle \cdot ,\cdot \right \rangle _X}\). Let \(X'\) be the dual space of \(X\) with respect to the duality pairing \(\left \langle \cdot ,\cdot \right \rangle \) 1.
Now we take the general self-adjoint second order differential operator \(L: X \rightarrow X'\) as an example. \begin{equation} \label {eq:diff-operator-2nd-order} (Lu)(x):= -\sum _{i,j=1}^d \frac {\pdiff }{\pdiff x_j} \left [ a_{ji}(x)\frac {\pdiff u}{\pdiff x_{i}} \right ] + a_0(x)u(x). \end{equation} Because \(L\) is self-adjoint, \(a_{ji}(x) = a_{ij}(x)\). Test \((Lu)(x)\) with \(v(x)\) and apply integration by parts in Theorem 3, we have \begin{equation} \begin {aligned} \int _{\Omega }(Lu)(x)v(x) \intd x &= \sum _{i,j=1}^d \int _{\Omega } a_{ji}(x)\frac {\pdiff u}{\pdiff x_{i}}\frac {\pdiff v}{\pdiff x_{j}} \intd x + \int _{\Omega } a_0(x)u(x)v(x) \intd x \\ & \quad - \sum _{i,j=1}^d\int _{\pdiff \Omega } \gamma _0^{\rm int}\left ( a_{ji}(x)\frac {\pdiff u}{\pdiff x_{i}} \right ) \gamma _0^{\rm int}v(x) n_j \intd s \\ &=\sum _{i,j=1}^d \int _{\Omega } a_{ji}(x)\frac {\pdiff u}{\pdiff x_{i}}\frac {\pdiff v}{\pdiff x_{j}} \intd x + \int _{\Omega } a_0(x)u(x)v(x) \intd x \\ & \quad -\int _{\pdiff \Omega } \gamma _0^{\rm int} \left [ \sum _{i,j=1}^d n_j a_{ji}(x)\frac {\pdiff u}{\pdiff x_{i}} \right ] \gamma _0^{\rm int}v(x) \intd s. \end {aligned} \end{equation} Define the interior conormal trace: \begin{equation} \label {eq:interior-conormal-trace} \gamma _1^{\rm int}u(x):= \lim _{\Omega \ni \tilde {x} \rightarrow x \in \pdiff \Omega } \left [ \sum _{i,j=1}^d n_j(x)a_{ji}(\tilde {x})\frac {\pdiff u(\tilde {x})}{\pdiff \tilde {x}_i} \right ]. \end{equation} Define the bilinear form \(a(u,v)\): \begin{equation} \label {eq:bilinear-form-2nd-order-pde} a(u,v):= \sum _{i,j=1}^d\int _{\Omega }a_{ji}(x)\frac {\pdiff u}{\pdiff x_{i}}\frac {\pdiff v}{\pdiff x_{j}}\intd x + \int _{\Omega }a_0uv \intd x. \end{equation} Because the original operator \(L\) is self-adjoint, \(a_{ji}(x) = a_{ij}(x)\), the bilinear form \(a(u,v)\) is symmetric. Then we have the general form of the Green’s first identity: \begin{equation} \label {eq:green-1st-identity-general} a(u,v) = \int _{\Omega } (Lu)(x)v(x) \intd x + \int _{\pdiff \Omega } \gamma _1^{\rm int}u(x) \gamma _0^{\rm int}v(x) \intd s. \end{equation} Because \(a(u,v) = a(v,u)\), we also have \begin{equation} a(v,u) = \int _{\Omega } (Lv)(x)u(x) \intd x + \int _{\pdiff \Omega } \gamma _1^{\rm int}v(x) \gamma _0^{\rm int}u(x) \intd s. \end{equation} Subtract it from Equation (30), we obtain the general form of the Green’s second identity: \begin{equation} \label {eq:green-2nd-identity-general} \int _{\Omega } (Lu)(x)v(x) \intd x - \int _{\Omega }(Lv)(x)u(x) \intd x = \int _{\pdiff \Omega }\gamma _1^{\rm int}v(x)\gamma _0^{\rm int}u(x) \intd s - \int _{\pdiff \Omega } \gamma _1^{\rm int}u(x)\gamma _0^{\rm int}v(x) \intd s. \end{equation} With duality pairing, these two Green’s identities can be written in a compact form as below. \begin{equation} \label {eq:green-1st-identity-compact} a(u,v) = \left \langle Lu, v \right \rangle _{\Omega } + \left \langle \gamma _1^{\rm int}u, \gamma _0^{\rm int}v \right \rangle _{\Gamma }. \end{equation} \begin{equation} \label {eq:green-2nd-identity-compact} \left \langle Lu, v \right \rangle _{\Omega } - \left \langle u, Lv \right \rangle _{\Omega } = \left \langle \gamma _1^{\rm int}v, \gamma _0^{\rm int}u \right \rangle _{\Gamma } - \left \langle \gamma _1^{\rm int}u, \gamma _0^{\rm int}v \right \rangle _{\Gamma }. \end{equation} Here we use the subscript \(\Omega \) to indicate volume integral and use the subscript \(\Gamma \) to indicate surface integral.
Specifically, when the coefficient \(a_{ji}\) is the Kronecker delta \(\delta _{ji}\) and \(a_0 = 0\), we obtain the negative Laplace operator \(-\Delta \). Hence the bilinear form is \begin{equation} a(u,v) = \int _{\Omega } \sum _{i=1}^d \frac {\partial u}{\partial x_i} \frac {\partial v}{\partial x_j} \intd x = \int _{\Omega } \grad u \cdot \grad v \intd x. \end{equation} The general Green’s first identity becomes \begin{equation} \label {eq:green-1st-identity-general-laplace} \int _{\Omega }\grad u\cdot \grad v \intd x = \int _{\Omega }-v\Delta u \intd x + \int _{\Omega } v \frac {\pdiff u}{\pdiff \vect {n}} \intd s, \end{equation} which is consistent with Equation (15).
The general Green’s second identity becomes \begin{equation} \left \langle \Delta u, v \right \rangle _{\Omega } - \left \langle u, \Delta v \right \rangle _{\Omega } = \left \langle \gamma _1^{\rm int}u, \gamma _0^{\rm int}v \right \rangle _{\Gamma } - \left \langle \gamma _1^{\rm int}v, \gamma _0^{\rm int}u \right \rangle _{\Gamma }, \end{equation} which is consistent with Equation (16).
References
Lawrence C. Evans. Partial Differential Equations. Graduate Studies in Mathematics ISBN: 9780821849743. American Mathematical Society. ISBN 978-0-8218-4974-3. URL https://book.douban.com/subject/4767375/.
Olaf Steinbach. Numerical Approximation Methods for Elliptic Boundary Value Problems: Finite and Boundary Elements. Springer Science & Business Media. ISBN 978-0-387-31312-2.
1Note the difference between inner product and duality pairing. The two operands in the former operation are both in \(X\), while in the latter operation, one is in \(X\) and the other is in \(X'\). That’s why \(\left \langle \cdot ,\cdot \right \rangle \) is called duality pairing.