Understanding about operator discretization

Contents

 1 Vectors in strong form and weak form
 2 Discretization of the inverse of an operator
 3 Discretization of a preconditioner
 4 Summary

1 Vectors in strong form and weak form

Let \(V\) and \(W\) be two Hilbert spaces. Let \(V_h\) be the finite dimensional subspace of \(V\) with the basis \(\left \{ \varphi _{1},\cdots ,\varphi _{n} \right \}\) and \(W_h\) be the finite dimensional subspace of \(W\) with the basis \(\left \{ \zeta _{1},\cdots ,\zeta _{p} \right \}\). Let \(W'\) be the dual space of \(W\) and \(W_h'\) be its finite dimensional subspace with the basis \(\left \{ \psi _{1},\cdots ,\psi _{m} \right \}\). Let \(A: V \rightarrow W\) be a bounded linear operator from \(V\) to \(W\) and \(A_h: V_h \rightarrow W_h\) be its finite dimensional approximation.

A function \(u_h\in V_h\) can be expanded as \(u_h=\sum _{i=1}^n u_i \varphi _i\). Its expansion coefficients make up the strong form vector \(\underline {u} = (u_1,\cdots ,u_n)^{\mathrm {T}}\) of \(u_h\). Here we explicitly write this vector as \(\underline {u}^{\mathrm {S}}\) to be differentiated from the weak form.

To discretize the operator \(A_h\), we need two steps:

1. Apply \(A_h\) to \(u_h\), which produces a function \(w_h\) in \(W_h\).

2. Project \(w_h\) to each basis function \(\psi _i\) of \(W_h'\).

The said projection is formed by duality pairing \(\left \langle \cdot ,\cdot \right \rangle _{W_h',W_h}\) ¹ and will produce a vector \(\underline {w}^{\mathrm {W}}\), which is the weak form of \(w_h\). This vector is not related to the expansion coefficients \(w_k\) of \(w_h\) in \(W_h\), i.e. \(w_h = \sum _{k=1}^p w_k\zeta _k\), but is the projection coefficients of \(w_h\) in the dual space \(W_h'\).

The expression for \(\underline {w}^{\mathrm {W}}\) can be expanded as \begin{equation} \underline {w}^{\mathrm {W}} = \begin {pmatrix} \left \langle \psi _1, w_h \right \rangle \\ \vdots \\ \left \langle \psi _m, w_h \right \rangle \end {pmatrix} = \begin {pmatrix} \left \langle \psi _1,A_hu_h \right \rangle \\ \vdots \\ \left \langle \psi _m,A_hu_h \right \rangle \end {pmatrix} = \begin {pmatrix} \left \langle \psi _1,A_h\sum _{j=1}^n u_j\varphi _j \right \rangle \\ \vdots \\ \left \langle \psi _m,A_h\sum _{j=1}^n u_j\varphi _j \right \rangle \end {pmatrix} = \begin {pmatrix} \sum _{j=1}^n \left \langle \psi _1, A_h \varphi _j \right \rangle u_j \\ \vdots \\ \sum _{j=1}^n \left \langle \psi _m, A_h \varphi _j \right \rangle u_j \end {pmatrix}. \end{equation} Its matrix form is \begin{equation} \underline {w}^{\mathrm {W}} = \mathcal {A} \underline {u}^{\mathrm {S}}, \end{equation} where \(\mathcal {A}_{ij} = \left \langle \psi _i, A_h\varphi _j \right \rangle \). If we substitute \(w_h = \sum _{k=1}^p w_k\zeta _k\) into the left hand side of this equation, we have \begin{equation} \underline {w}^{\mathrm {W}} = \begin {pmatrix} \left \langle \psi _1, \sum _{k=1}^p w_i\zeta _k \right \rangle \\ \vdots \\ \left \langle \psi _m, \sum _{k=1}^p w_i\zeta _k \right \rangle \end {pmatrix} = \begin {pmatrix} \sum _{k=1}^p \left \langle \psi _1, \zeta _k \right \rangle w_k \\ \vdots \\ \sum _{k=1}^p \left \langle \psi _m, \zeta _k \right \rangle w_k \\ \end {pmatrix} = \begin {pmatrix} \sum _{j=1}^n \left \langle \psi _1, A_h \varphi _j \right \rangle u_j \\ \vdots \\ \sum _{j=1}^n \left \langle \psi _m, A_h \varphi _j \right \rangle u_j \end {pmatrix}. \end{equation} Its matrix form is \begin{equation} \underline {w}^{\mathrm {W}} = \mathcal {M}_{W_h',W_h} \underline {w}^{\mathrm {S}} = \mathcal {A} \underline {u}^{\mathrm {S}}. \end{equation} In this equation, \(\mathcal {M}_{W_h',W_h}\) is the mass matrix associated with the duality pairing between the dual space \(W_h'\) and the range space \(W_h\) with respect to the operator \(A\) ². For simplicity, this matrix is written as \(\mathcal {M}_A\).

The vector \(\underline {w}^{\mathrm {S}}\) contains the actual expansion coefficients \((w_{1},\cdots ,w_{p})^{\mathrm {T}}\) of \(w_h\) in \(W_h\), therefore it is the strong form of \(w_h\), which can be derived from the weak form of \(w_h\) as below: \begin{equation} \underline {w}^{\mathrm {S}} = \mathcal {M}_A^{-1} \underline {w}^{\mathrm {W}} = \mathcal {M}_A^{-1}\mathcal {A}\underline {u}^{\mathrm {S}}. \end{equation} This means the mass matrix \(\mathcal {M}_A\) should be a square matrix and invertible, which requires two conditions:

1. The number of basis elements adopted for the range space \(W_h\) of \(A\) should be the same as that for the dual space \(W_h'\).

   Take the single layer potential (SLP) operator \(V: H^{-1/2}(\Gamma ) \rightarrow H^{1/2}(\Gamma )\) in BEM as an example. \(W\) is \(H^{1/2}(\Gamma )\) and \(W'\) is \(H^{-1/2}(\Gamma )\). \(W_h\) is usually the piecewise linear continuous function space and \(W_h'\) is the piecewise constant function space. Basis functions of the former space are configured at nodes in the mesh, while basis functions for the latter space are configured in cells. Therefore, the number of basis functions of the two spaces usually mismatch. The remedy is to construct the space \(W_h'\) on the dual mesh, then there is a one-to-one correspondence between each cell in the dual mesh and each node in the primal mesh.

2. The duality pairing between \(W_h'\) and \(W_h\) should be \(\inf \sup \) stable in the sense that the following condition should be satisfied (Betcke et al.) \begin{equation} \inf _{u\in W_h} \sup _{v\in W_h'} \frac {\lvert \left \langle u,v \right \rangle \rvert }{\lVert u \rVert _{W_h} \lVert v \rVert _{W_h'}} \geq c > 0. \end{equation}

Then the mass matrix \(\mathcal {M}_A\) is invertible.

This \(\inf \sup \) stability is just the unique solvability condition or well-posedness condition of the following variational formulation: given \(f\in V'\), find \(u\in U\), such that \begin{equation} a(u,v) = \left \langle f, v \right \rangle \quad \forall v\in V. \end{equation} Such a variational formulation involves the generalized bilinear form \(a(\cdot ,\cdot ): U\times V \rightarrow \mathbb {R}\), where the two component spaces \(U\) and \(V\) are different. Therefore, this condition is a generalization of the ellipticity condition involved in the Lax-Milgram Lemma, where the bilinear form requires two identical spaces.

For the duality pairing \(\left \langle \cdot ,\cdot \right \rangle _{W_h', W_h}\), it is actually a bilinear form \(a(\cdot ,\cdot ): W_h\times W_h' \rightarrow \mathbb {R}\) defined as \(a(u,v) := \left \langle v, Iu \right \rangle \), where \(I: W_h \rightarrow W_h\) is the identity operator. If the \(\inf \sup \) condition is satisfied, the mass matrix, as a discretization of the operator \(I\), is invertible.

2 Discretization of the inverse of an operator

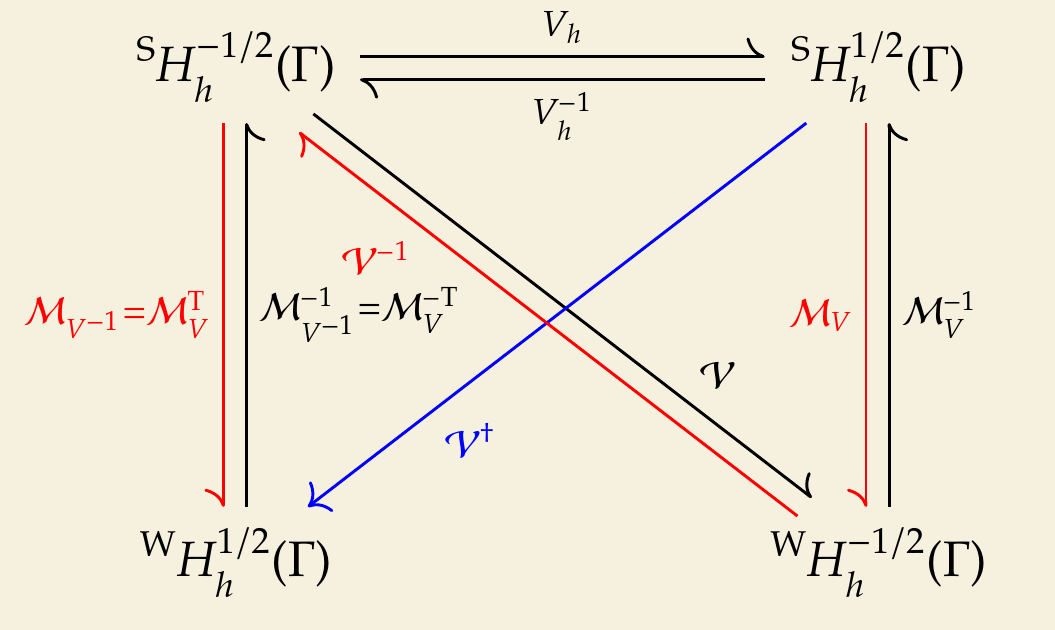
In BEM, when there is source distribution \(f\in \tilde {H}^{-1}(\Omega )\) in the volume domain \(\Omega \), the Newton potential \(N_0 f\) will also contribute to the Neumann trace at the boundary \(\Gamma \) as \(V^{-1}(N_0 f)\), where \(N_0: \tilde {H}^{-1}(\Omega ) \rightarrow H^{1/2}(\Gamma )\) and \(V^{-1}: H^{1/2}(\Gamma ) \rightarrow H^{-1/2}(\Gamma )\). It is obvious that if somehow we can directly discretize the inverse SLP operator \(V^{-1}\) into a matrix \(\mathcal {V}^{\dagger }\), its row and column function spaces are \(^{\mathrm {W}}H_h^{1/2}(\Gamma )\times ^{\mathrm {S}}H_h^{1/2}(\Gamma )\). On the other hand, if the matrix for \(V\) is \(\mathcal {V}\) and \(\mathcal {V}^{-1}\) is its inverse matrix, the row and column function spaces of \(\mathcal {V}^{-1}\) are \(^{\mathrm {S}}H_h^{-1/2}(\Gamma )\times ^{\mathrm {W}}H_h^{-1/2}(\Gamma )\). Therefore, \(\mathcal {V}^{\dagger }\) and \(\mathcal {V}^{-1}\) are two different matrices. N.B. Even though the function spaces related to matrices \(\mathcal {V}\) and \(\mathcal {V}^{-1}\) are the same \(H_h^{-1/2}(\Gamma )\times H_h^{-1/2}(\Gamma )\), the input or output vectors of the two matrices have different identities in the sense of strong or weak.

In practice, an inverse operator like \(V^{-1}\) cannot be directly evaluated or discretized. We can only compute an approximation \(\tilde {\mathcal {V}^{\dagger }}\) of \(\mathcal {V}^{\dagger }\) by starting from the inverse of the matrix for the original operator, which is \(\mathcal {V}^{-1}\). In \(V^{-1}(N_0f)\), \(N_0f\) directly returns a strong form vector in \(H_h^{1/2}(\Gamma )\), which is the column space of the matrix \(\tilde {\mathcal {V}^{\dagger }}\). Hence we need to project this strong form vector from \(H_h^{1/2}(\Gamma )\) to the weak column space \(H_h^{-1/2}(\Gamma )\) of \(\mathcal {V}^{-1}\), and we can call this operation as space adaptation. This can be directly achieved by multiplying the mass matrix \(\mathcal {M}_{V}\) induced by the duality pairing between \(H_h^{-1/2}(\Gamma )\) and \(H_h^{1/2}(\Gamma )\). The output from \(\mathcal {V}^{-1}\) is a strong form vector in \(H_h^{-1/2}(\Gamma )\), which should be further mapped to the weak row space \(H_h^{1/2}(\Gamma )\) of \(\mathcal {V}^{\dagger }\). Because this is also a direct projection of a strong form vector to a weak form vector, we need to multiply the mass matrix \(\mathcal {M}_{V^{-1}}\) induced by the duality pairing between \(H_h^{1/2}(\Gamma )\) and \(H_h^{-1/2}(\Gamma )\).

Let the basis of \(H_h^{1/2}(\Gamma )\) be \(\left \{ \varphi _{1},\cdots ,\varphi _{n} \right \}\) and the basis of \(H_h^{-1/2}(\Gamma )\) be \(\left \{ \psi _{1},\cdots ,\psi _{m} \right \}\). The coefficients of the above two mass matrices are \begin{equation} \mathcal {M}_V[i,j] = \left \langle \psi _i,\varphi _j \right \rangle \quad i=1,\cdots ,m, j=1,\cdots ,n \end{equation} and \begin{equation} \mathcal {M}_{V^{-1}}[i,j] = \left \langle \varphi _i,\psi _j \right \rangle \quad i=1,\cdots ,n, j=1,\cdots ,m. \end{equation} Therefore, \(\mathcal {M}_V = \mathcal {M}_{V^{-1}}^{\mathrm {T}}\). The matrix \(\tilde {\mathcal {V}}^{\dagger }\) as an approximate discretization of the inverse operator \(V^{-1}\) is \begin{equation} \tilde {\mathcal {V}^{\dagger }} = \mathcal {M}_V^{\mathrm {T}} \mathcal {V}^{-1} \mathcal {M}_V. \end{equation} The commutative diagram for the above operators and matrices is shown below, where the red route indicates the computation of \(\tilde {\mathcal {V}^{\dagger }}\) as the approximation for \(\mathcal {V}^{\dagger }\).

Another example is the discretization of the Steklov-Poincaré operator in the symmetric form for the interior problem: \begin{equation} S = D + \left ( \frac {1}{2}I_1 + K' \right ) V^{-1} \left ( \frac {1}{2}I_2 + K \right ), \end{equation} where the mapping properties of involved operators are \begin{equation} \begin {aligned} S, D &: H^{1/2}(\Gamma ) \rightarrow H^{-1/2}(\Gamma ) \\ I_1, K' &: H^{-1/2}(\Gamma ) \rightarrow H^{-1/2}(\Gamma ) \\ V^{-1} &: H^{1/2}(\Gamma ) \rightarrow H^{-1/2}(\Gamma ) \\ I_2, K &: H^{1/2}(\Gamma ) \rightarrow H^{1/2}(\Gamma ) \end {aligned}. \end{equation} Let \(\mathcal {M}\) be the mass matrix between \(H^{-1/2}(\Gamma )\) and \(H^{1/2}(\Gamma )\), we have the matrix form for \(S\) as \begin{equation} \mathcal {S} = \mathcal {D} + \left ( \frac {1}{2}\mathcal {M}^{\mathrm {T}} + \mathcal {K}^{\mathrm {T}} \right ) \mathcal {M}^{-\mathrm {T}} \mathcal {M}^{\mathrm {T}} \mathcal {V}^{-1} \mathcal {M} \mathcal {M}^{-1} \left ( \frac {1}{2}\mathcal {M} + \mathcal {K} \right ) = \mathcal{D} + \left ( \frac {1}{2}\mathcal {M}^{\mathrm {T}} + \mathcal {K}^{\mathrm {T}} \right ) \mathcal {V}^{-1} \left ( \frac {1}{2}\mathcal {M} + \mathcal {K} \right ), \end{equation} which follows the red route in the following commutative diagram.

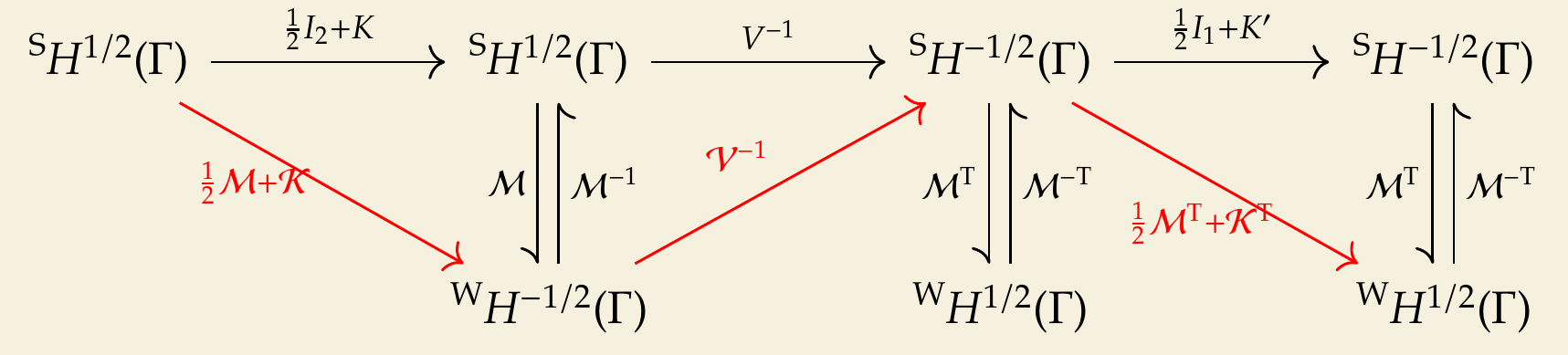
3 Discretization of a preconditioner

When an iterative solver is used in BEM, only matrix/vector multiplication is needed. Therefore, the stiffness matrix \(\mathcal {S}\) associated with the Steklov-Poincaré operator \(S\) is not assembled explicitly, while each of its component matrix that constitutes \(S\) except the inverse matrix \(\mathcal {V}^{-1}\) will be assembled, i.e. \(\mathcal {D}\) and \(\frac {1}{2}\mathcal {M} + \mathcal {K}\). Let the input vector of \(\mathcal {S}\) be \(\underline {u}\) and the result of \(\left ( \frac {1}{2}\mathcal {M} + \mathcal {K} \right ) \underline {u}\) be \(\underline {b}\). Then computing \(\mathcal {V}^{-1} \underline {b}\) is equivalent to solving \(\mathcal {V} \underline {x} = \underline {b}\) for \(\underline {x}\). During the solution of this equation, \(\mathcal {V}\) should be preconditioned. Using the concept of operator preconditioning (Mardal and Winther), the preconditioning operator for \(V\) is \(I + D\), due to the fact that \((I+D)^{-1}\) is spectrally equivalent to \(V\) (Hsiao et al.). Then the matrix corresponding to \((I+D)^{-1}\) is the preconditioning matrix, whose inverse will be applied to the two sides of \(\mathcal {V}\underline {x} = \underline {b}\). Compared to multigrid and multilevel preconditioning techniques, operator preconditioning has two advantages:

1. It does not rely on a hierarchical mesh, which is much easier to implement.

2. There is a rigorous proof about spectral equivalence, so the condition number of the preconditioned system can be controlled uniformly independent of the mesh size.

N.B. The preconditioning operator corresponds to the inverse of the preconditioning matrix.

With the conclusion for the discretization of an inverse operator, the approximate matrix for \((I+D)^{-1}\) is \begin{equation} \mathcal {M}_D^{\mathrm {T}} (\tilde {\mathcal {M}} + \mathcal {D})^{-1} \mathcal {M}_D, \end{equation} where \(\mathcal {M}_D\) is the mass matrix related to the duality pairing \(\left \langle \cdot ,\cdot \right \rangle _{H_h^{1/2}(\Gamma ), H_h^{-1/2}(\Gamma )}\) between the dual space and range space of the operator \(D\), \(\tilde {\mathcal {M}}\) is the mass matrix related to the inner product in \(H^{1/2}(\Gamma )\), since its row space and column space are the same space \(H^{1/2}(\Gamma )\). The row space of \(\mathcal {M}_D^{\mathrm {T}} (\tilde {\mathcal {M}} + \mathcal {D})^{-1} \mathcal {M}_D\) is the dual space of the domain space of the operator \(I+D\), i.e. \(^{\mathrm {W}}H^{-1/2}(\Gamma )\). Its column space is the range space of \(I+D\), i.e. \(^{\mathrm {S}}H^{-1/2}(\Gamma )\). Therefore, the preconditioning matrix is a square matrix.

The inverse of the preconditioning matrix is \begin{equation} \mathcal {M}_D^{-1} (\tilde {\mathcal {M}} + \mathcal {D}) \mathcal {M}_D^{-\mathrm {T}}, \end{equation} which is to be multiplied to \(\mathcal {V}\) from left. Its row and column spaces are \(^{\mathrm {S}}H^{-1/2}(\Gamma )\times ^{\mathrm {W}}H^{-1/2}(\Gamma )\). We also notice that the function spaces for the preconditioned matrix \(\mathcal{M}_D^{-1} (\tilde{\mathcal{M}} + \mathcal{D}) \mathcal{M}_D^{-\mathrm{T}} \mathcal {V}\) are \(^{\mathrm {S}}H^{-1/2}(\Gamma )\times ^{\mathrm {S}}H^{-1/2}(\Gamma )\), i.e. its row and column spaces are both in the strong form.

The above example is special in that the preconditioning operator \(I+D\) is explicitly known and can be evaluated. Therefore, there is no need to build the matrix for \((I+D)^{-1}\) first, then compute its inverse. Instead, we can directly build the inverse of the preconditioning matrix using the rule of product algebra (Betcke et al.) for discretizing a composition of operators \((I+D)V\). Its matrix form is \begin{equation} (\tilde {\mathcal {M}} + \mathcal {D}) \mathcal {M}_V^{-1} \mathcal {V}, \end{equation} where \(\mathcal {M}_V\) is the duality pairing between the dual and range space of the operator \(V\), which is just the transpose of \(\mathcal {M}_D\). The row space of \(\tilde {\mathcal {M}} + \mathcal {D}\) is \(^{\mathrm {W}}H_h^{1/2}(\Gamma )\), which is the dual space of the range space of the operator \(I+D\), i.e. \(^{\mathrm {S}}H^{-1/2}(\Gamma )\). However, as we mentioned above, the row and column spaces of a preconditioned matrix should be in the strong form, and the row space should be the range space of the operator \(I+D\). Therefore, we need to perform another weak form to strong form transformation via the inverse of the matrix \(\mathcal {M}_D\). Finally, we obtain \begin{equation} \mathcal {M}_D^{-1} (\tilde {\mathcal {M}} + \mathcal {D}) \mathcal {M}_D^{-\mathrm {T}} \mathcal {V} \end{equation} and the inverse of the preconditioning matrix is \(\mathcal {M}_D^{-1} (\tilde {\mathcal {M}} + \mathcal {D}) \mathcal {M}_D^{-\mathrm {T}}\). This result is the same as the previous method. The commutative diagram is as below.

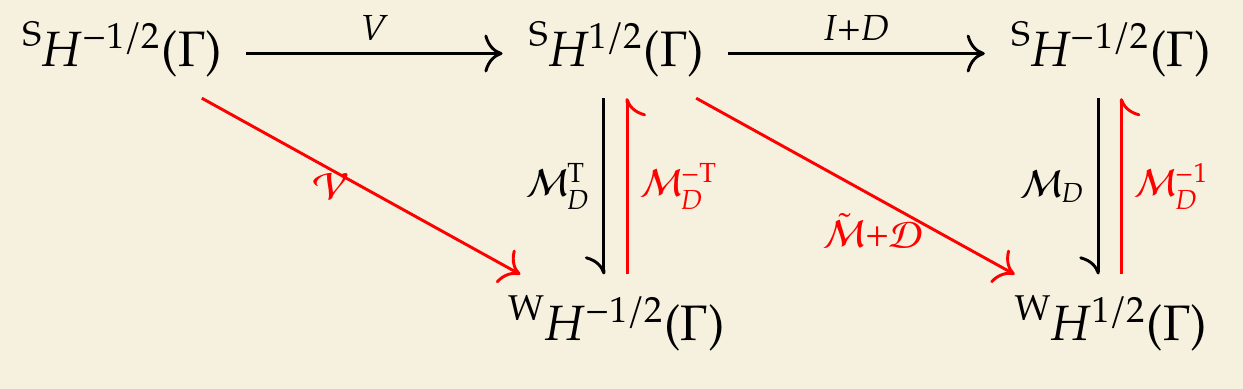
4 Summary

In BEM, the Galerkin discretization of an operator and its input and output functions involve the concept of strong and weak form. The transformation between such strong form and weak form is realized via the duality pairing between the range space and dual space of the operator. Even though, the matrix obtained from operator discretization hides the range space, when the inverse of an operator is to be discretized, such range space emerges to the surface. If we want to build a preconditioner using operator preconditioning technique, such problem will also arise.

Following is a list of key points to be kept in mind:

1. The Galerkin discretization of an operator produces a matrix which involves the domain space and dual space of the operator, while the range space is implicit.

2. The input vector of the matrix is a strong form vector in the domain space, which is associated with the column space of the matrix.

3. The output vector of the matrix is a weak form vector in the dual space of the operator’s range space, which is associated with the row space of the matrix. The weak form vector can be considered as a direct projection from the implicit range space to its dual space via duality paring.

4. To get the strong form vector related to the output function of the operator, we need to further multiply the inverse of the mass matrix associated with the duality pairing to the weak form vector. This is inverse mass matrix is the discretization of the Riesz map mentioned in (Betcke et al.).

5. The Galerkin matrix for the inverse of an operator maps a strong form vector in the range space of the original operator to a weak form vector in the dual space of the domain space.

6. The inverse of the Galerkin matrix for an operator maps a weak form vector in the dual space of the range space to a strong form vector in the domain space.

7. The row and column spaces of a preconditioned matrix are both in the strong form.

References

   Timo Betcke, Matthew Scroggs, and Wojciech Smigaj. Product algebras for galerkin discretisations of boundary integral operators and their applications. URL http://arxiv.org/abs/1711.10607.

   G. C. Hsiao, O. Steinbach, and W. L. Wendland. Domain decomposition methods via boundary integral equations. 125(1):521–537. ISSN 0377-0427. doi: 10.1016/S0377-0427(00)00488-X.

   Kent-Andre Mardal and Ragnar Winther. Preconditioning discretizations of systems of partial differential equations. 18(1):1–40. ISSN 1099-1506. doi: 10.1002/nla.716.

¹If there is no ambiguity from the context, we can simply write the duality pairing as \(\left \langle \cdot ,\cdot \right \rangle \) without indicating the primal and dual space.

²When specifying the function spaces related to a matrix, we put the row space in front of the column space.

Backlinks: 《Spectral equivalence》