Understanding about Riesz map
Contents
2 Construction of the Riesz map as a preconditioner
2.1 Riesz map to be used as a preconditioner depends on the definition of inner product
2.2 Riesz map as a baseline preconditioner
3 Construction of the Riesz map as a space adaptor
3.1 Issue of implicit range spaces in BEM
3.2 Mass matrix as space projection
3.3 Riesz map for transforming a function from dual space to range space
1 Riesz representation theorem (Brezis)
Theorem 1 (Riesz-Fréchet representation theorem) Let \(H\) be a Hilbert space and \(H'\) be its dual space. \(\left ( \cdot ,\cdot \right )\) is the inner product on \(H\). \(\left \langle \cdot ,\cdot \right \rangle \) is the duality pairing between \(H\) and \(H'\). Given any \(f \in H'\), there exits a unique \(u \in H\) such that \begin{equation} \label {eq:riesz-representation} \left \langle f,v \right \rangle = \left ( u,v \right ) \quad \forall v\in H \end{equation} and \(\lVert f \rVert _{H'} = \lVert u \rVert _H\).
2 Construction of the Riesz map as a preconditioner
2.1 Riesz map to be used as a preconditioner depends on the definition of inner product
The two functions in the duality pairing on the left hand side of Equation (1) have different roles: \(f\) is the bounded linear functional and \(v\) is the object to be operated by it. The two functions \(u\) and \(v\) in the inner product on the right hand side have the same identity. This theorem states that there is an isometric isomorphism between a Hilbert space and its dual space.
Riesz map is a map from the dual space \(H'\) to the primal space \(H\), i.e. \(\tau : H' \rightarrow H\). Hence, the Riesz-Fréchet theorem can be written as \begin{equation} \left ( \tau f, v \right ) = \left \langle f, v \right \rangle \quad \forall v \in H \end{equation} and \(\lVert \tau f \rVert _H = \lVert f \rVert _{H'}\). The Riesz map depends on the definition of the inner product on \(H\). Here are three examples.
-
Use the canonical \(L_2\) inner product on \(H\). Then \begin{equation} \left ( \tau f, v \right ) = \int _{\Omega } (\tau f) v \intd x. \end{equation} Equate it to the duality pairing \(\left \langle f, v \right \rangle \): \begin{equation} \int _{\Omega } (\tau f) v \intd x = \left \langle f, v \right \rangle \quad \forall v\in H. \end{equation} If we treat \(\tau f\) (as a whole) as the solution to be sought, this equation is actually in the weak form or variational form. By introducing the identity operator \(I: H \rightarrow H'\), the integral on the left hand side can be written as a bilinear form, \begin{equation} \left \langle I (\tau f), v \right \rangle = \left \langle f, v \right \rangle \quad \forall v\in H. \end{equation} The strong form or operator form of the equation is \begin{equation} I (\tau f) = f. \end{equation} Then the Riesz map \(\tau \) is the inverse operator of \(I\), i.e. \(I^{-1}\).
Now we want to see the discretized matrix form of the operators \(I\) and \(\tau \). The discretization is carried out using the Galerkin method. Let \(H_h\) be a finite dimensional subspace of the primal space \(H\) with the basis \(\left \{\varphi _1,\cdots ,\varphi _n \right \}\), and \(H_h'\) be a finite dimensional subspace of the dual space \(H'\) with the basis \(\left ( \psi _1,\cdots ,\psi _m \right )\). The matrix for \(I\) is \begin{equation} \mathcal {M}_{ij} = \left \langle I\varphi _j, \varphi _i \right \rangle = \left ( \varphi _j, \varphi _i \right ), \end{equation} and the matrix for \(\tau \) is \(\mathcal {M}^{-1}\).
Comment 1 Here we directly use the matrix coefficient \(\mathcal {M}_{ij}\) as a representation of the whole matrix \(\mathcal {M}\). Such a representation is unambiguous and is consistent with the convention for writing tensors in differential geometry. Because \(I\) maps \(\varphi _j\) in \(H\) to a same function in \(H'\), the duality pairing of \(I\varphi _j\) and \(\varphi _i\) is actually the \(L_2\) inner product of \(\varphi _j\) and \(\varphi _i\).
-
If \(H\) is the Sobolev space \(H_0^1(\Omega )\), we can use the inner product inherited from \(H^1(\Omega )\): \begin{equation} \left ( u,v \right )_{H^1(\Omega )} = \int _{\Omega } \left ( \nabla u \cdot \nabla v + uv \right ) \intd x. \end{equation} Then the left hand side of Equation (1) is \begin{equation} \left ( \tau f, v \right ) = \int _{\Omega } \left ( \nabla (\tau f)\cdot (\nabla v) + (\tau f) v \right ) \intd x. \end{equation} The corresponding weak form is \begin{equation} \left ( \tau f, v \right ) = \int _{\Omega } \left ( \nabla (\tau f)\cdot (\nabla v) + (\tau f) v \right ) \intd x = \left \langle f, v \right \rangle \quad \forall v\in H. \end{equation} Its strong form is \begin{equation} -\Delta (\tau f) + \tau f = f, \end{equation} i.e. \begin{equation} \left ( -\Delta + I \right )(\tau f) = f. \end{equation} This is just the Helmholtz equation and \(\tau f\) is its solution. Solving \(\tau f\) for this equation with the given data \(f\) has the same effect as the Riesz map \(\tau \). Therefore, using the above inner product, the Riesz map is the inverse of the Helmholtz operator.
The matrix derived from the weak form of the Helmholtz operator is \begin{equation} \mathcal {H}_{ij} = \int _{\Omega } \left ( \nabla \varphi _j \cdot \nabla \varphi _i + \varphi _j \varphi _i \right ) \intd x. \end{equation} The matrix for \(\tau \) is \(\mathcal {H}^{-1}\). \(\mathcal {H}\) can also be understood as a new mass matrix with respect to the above inner product.
-
In this case, \(H\) is still \(H_0^1(\Omega )\), but the inner product becomes \begin{equation} \left ( u,v \right )_{H^1(\Omega )} = \int _{\Omega } \nabla u \cdot \nabla v \intd x. \end{equation} This inner product induces the semi-norm on \(H^1(\Omega )\), which is also a norm on \(H_0^1(\Omega )\).
The weak form equation is \begin{equation} \int _{\Omega } \nabla (\tau f) \cdot (\nabla v) \intd x = \left \langle f, v \right \rangle \quad \forall v\in H. \end{equation} The strong form is \begin{equation} -\Delta (\tau f) = f. \end{equation} This is just the Poisson equation. Riesz map \(\tau \) is the inverse of the Laplace operator. The matrix for the Laplace operator is \begin{equation} \mathcal {L}_{ij} = \int _{\Omega } \nabla \varphi _j \cdot \nabla \varphi _i \intd x. \end{equation} Similarly, \(\mathcal {L}\) can be understood as a mass matrix with respect to the above inner product. The matrix for \(\tau \) is \(\mathcal {L}^{-1}\).
2.2 Riesz map as a baseline preconditioner
From above we can see that the Riesz map from \(H'\) to \(H\) is actually the inverse of a differential operator \(\tilde {A}: H \rightarrow H'\), or it can also be understood as a kind of mass matrix which depends on the inner product adopted for \(H\). According to (Mardal and Winther), a preconditioner \(B\) is an isomorphism from \(H'\) to \(H\). Therefore, the Riesz map can be considered as a preconditioner, even though it is not optimal according to (Kirby).
Since a Riesz map is the inverse of \(\tilde {A}\), its matrix form usually cannot be directly assembled. We can first assemble the matrix \(\widetilde {\mathcal {A}}\) for the operator \(\tilde {A}\), then compute the approximate inverse of \(\widetilde {\mathcal {A}}\). In practice, when we use a preconditioner in an iterative solver, only matrix/vector multiplication is needed and a direct computation of matrix inverse is avoided. Instead, the linear system \(\widetilde {\mathcal {A}}x = y\) is to be solved, which has the same effect as \(\tilde {\mathcal {A}}^{-1}y\).
Comment 2 As an operator, the Riesz map \(\tau \) maps from \(H'\) to \(H\). As an inverse matrix \(\tilde {\mathcal {A}}^{-1}\), the matrix \(\tau \) have row and column spaces as \((H_h, H_h)\) 1 . At the first glance, it seems that the matrix spaces \(\left ( H_h,H_h \right )\) do not match the operator spaces \(H' \rightarrow H\). However, this is actually correct, since \(\tilde {\mathcal {A}}\) is derived from the weak form of the differential operator \(\tilde {A}\), whose row and column spaces are \(\left ( H_h,H_h \right )\). These spaces are just the same as those of the stiff matrix of the PDE. Therefore, the matrix for the Riesz map can be directly applied to the stiff matrix as a preconditioner.
3 Construction of the Riesz map as a space adaptor
3.1 Issue of implicit range spaces in BEM
In (Betcke et al.), product algebra is proposed for handling the discretization of the composition of two operators used in BEM. Being different from FEM, BEM has the issue of implicit range spaces (Domain, range and dual spaces in BEM). When there is a composition of two operators \(BA\), \(C=BA\) cannot be discretized as a whole usually. Then it is natural for us to build the two matrices for \(A\) and \(B\) first. Then we use \(\mathcal {A}\) and \(\mathcal {B}\) to construct the matrix \(\mathcal {C}\) for \(C\). However, \(\mathcal {C}\) is usually not a direct product of \(\mathcal {A}\) and \(\mathcal {B}\). Actually, after discretization, the range space of \(A\) is hidden and the test space of \(A\), which is the row space of \(\mathcal {A}\) does not match the domain space of \(B\), which is the column space of \(\mathcal {B}\).
3.2 Mass matrix as space projection
Definitions of the operators and matrices which are related to \(BA\):
-
\(A: \mathcal {H}_A^{\mathrm {dom}} \rightarrow \mathcal {H}_A^{\mathrm {ran}}\);
-
\(B: \mathcal {H}_{B}^{\mathrm {dom}} \rightarrow \mathcal {H}_{B}^{\mathrm {ran}}\) with \(\mathcal {H}_{A}^{\mathrm {ran}} \subset \mathcal {H}_{B}^{\mathrm {dom}}\), which makes the composition of \(A\) and \(B\) meaningful;
-
The identity maps \(M_A\) and \(M_B\) from the corresponding range space to dual space;
-
The mass matrices \(\mathcal {M}_A\) and \(\mathcal {M}_B\) associated with the identity maps;
-
The Riesz maps \(M_A^{-1}\) and \(M_B^{-1}\) as the inverse maps of \(M_A\) and \(M_B\) respectively;
-
The matrices for the Riesz maps \(\mathcal {M}_A^{-1}\) and \(\mathcal {M}_B^{-1}\).
The following commutative diagram shows the relationship between function spaces, when we are dealing with the discretization of \(BA\).
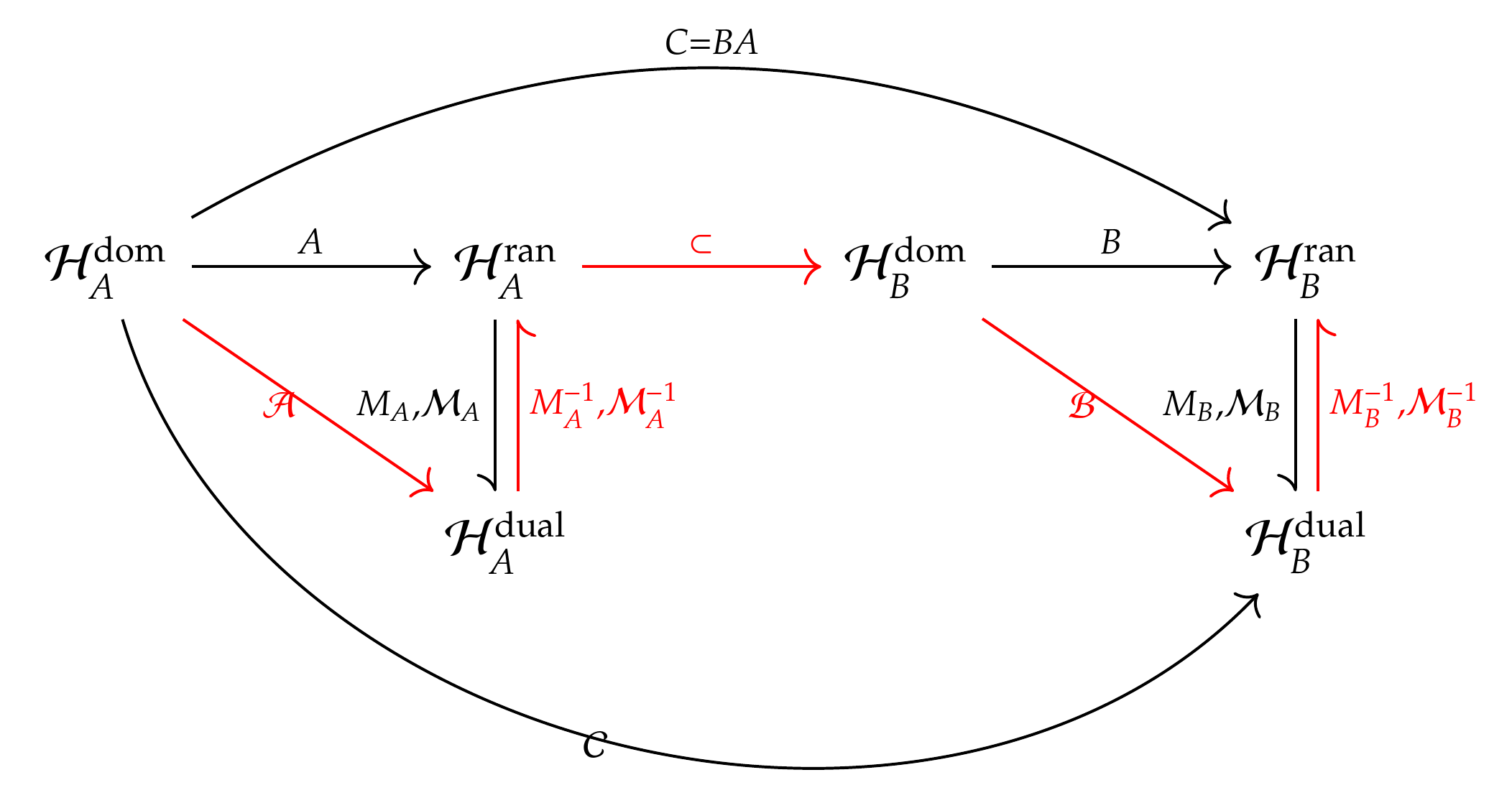
Taking the operator \(A\) as example. Let \(\left \{ \varphi _1,\cdots ,\varphi _n \right \}\) be the basis of the finite dimensional subspace \(\mathcal {V}_h^{\mathrm {ran}}\) of the range space \(\mathcal {H}_A^{\mathrm {ran}}\). Let \(\left \{ \psi _1,\cdots ,\psi _m \right \}\) be the basis of the finite dimensional subspace \(\mathcal {V}_h^{\mathrm {dual}}\) of the dual space \(\mathcal {H}_A^{\mathrm {dual}}\). Then the mass matrix \(\mathcal {M}_A\) is \begin{equation} \left ( \mathcal {M}_A \right )_{ij} = \left \langle \varphi _j, \psi _i \right \rangle . \end{equation} This is the projection of each basis function in the range space to each basis function in the dual space. The formulation of this mass matrix involves two different spaces and the projection of basis function is evaluated via the duality pairing. However, when the Riesz map is used as a preconditioner as in Section 2, the mass matrix involves only the primal space without its dual and the projection of basis function is evaluated via the inner product.
3.3 Riesz map for transforming a function from dual space to range space
The Riesz map \(M_A^{-1}: \mathcal {H}_A^{\mathrm {dual}} \rightarrow \mathcal {H}_{A}^{\mathrm {ran}}\) is the inverse of the identity operator from the range space to the dual space. For short, we write it as \(M_A^{-1}: H' \rightarrow H\). The associated matrix \(\mathcal {M}_A^{-1}\) have row and column spaces as \(\left ( H_h, H_h' \right )\), which are compatible with the operator spaces. This is different from the case when the Riesz map is used as a preconditioner.
By following the red route in the above diagram, the matrix \(\mathcal {C}\) can be obtained as \begin{equation} \mathcal {C}=\mathcal {B} \mathcal {M}_A^{-1} \mathcal {A}. \end{equation} Let \(u\) be a function in \(\mathcal {H}_{A}^{\mathrm {dom}}\). In the finite dimensional subspace, its associated vector is \(\vect {u}\). Then applying \(\mathcal {C}\) to \(\vect {u}\), we obtain a vector in the weak form, i.e. in the dual space \(\mathcal {H}_{B}^{\mathrm {dual}}\): \begin{equation} \mathcal {B} \mathcal {M}_A^{-1} \mathcal {A} \vect {u}. \end{equation} If we further apply the Riesz matrix \(\mathcal {M}_B^{-1}\), we have the vector in the strong form, i.e. in the range space \(\mathcal {H}_{B}^{\mathrm {ran}}\): \begin{equation} \mathcal {M}_B^{-1} \mathcal {B} \mathcal {M}_A^{-1} \mathcal {A} \vect {u}. \end{equation}
References
Timo Betcke, Matthew Scroggs, and Wojciech Smigaj. Product algebras for galerkin discretisations of boundary integral operators and their applications. URL http://arxiv.org/abs/1711.10607.
Haim Brezis. Functional Analysis, Sobolev Spaces and Partial Differential Equations. Springer. ISBN 978-0-387-70913-0 978-0-387-70914-7. doi: 10.1007/978-0-387-70914-7.
Robert C. Kirby. From functional analysis to iterative methods. 52(2):269–293. ISSN 0036-1445. doi: 10.1137/070706914.
Kent-Andre Mardal and Ragnar Winther. Preconditioning discretizations of systems of partial differential equations. 18(1):1–40. ISSN 1099-1506. doi: 10.1002/nla.716.
1Here we write the row space in front of the column space for a matrix as the Galerkin discretization of an operator.
Backlinks: 《Adjoint operators in functional analysis》