Different types of convergence
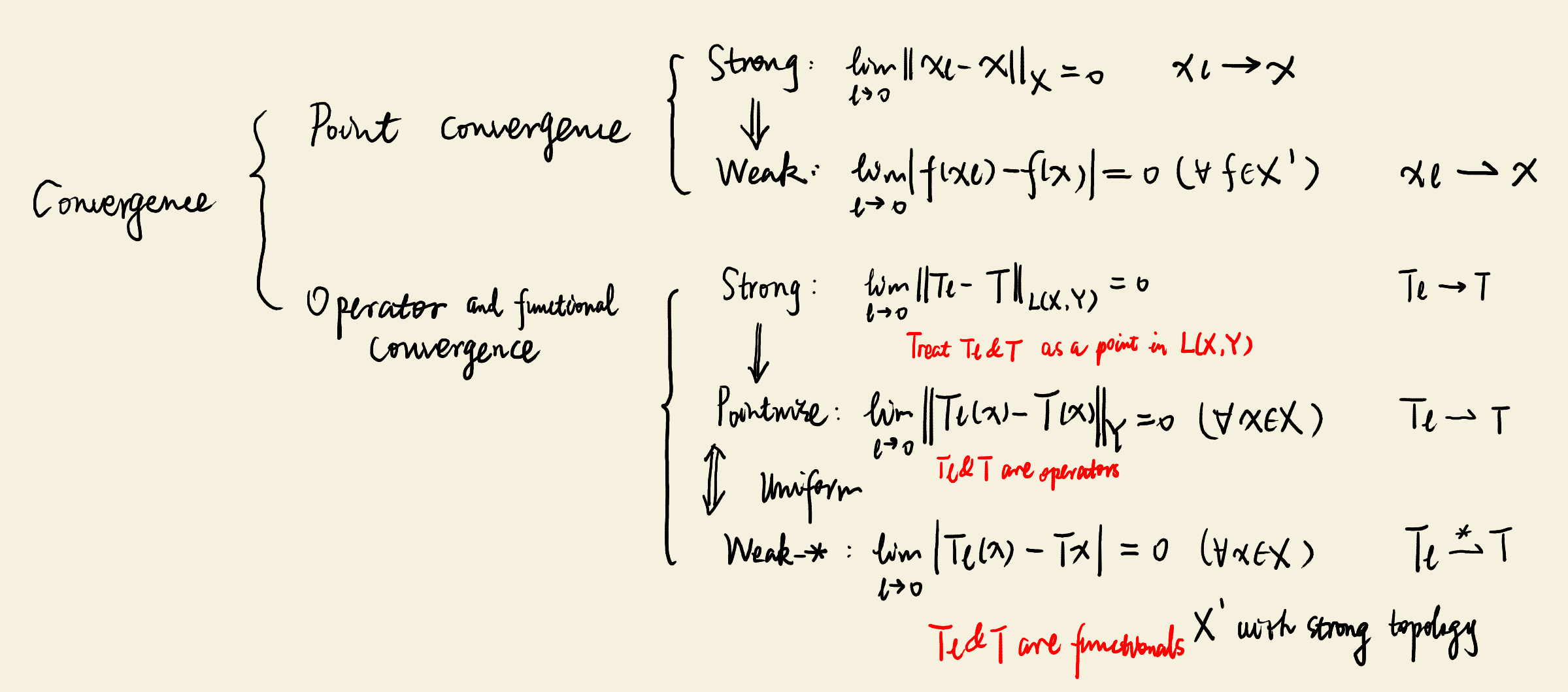
In functional analysis, several types of convergence are defined, namely,
- strong convergence for elements in normed linear space.
- weak convergence for elements in normed linear space, which is defined via the assistance of the dual space.
- weak-* convergence for linear functionals in the strong dual space of a normed linear space.
- pointwise convergence for functions
- uniform convergence for functions
Their definitions and differences are summarized below.
-
Definition (Strong convergence) Let \(X\) be a normed linear space and \((x_l)_{l \in \mathbb{N}}\) be a sequence in \(X\). Then \((x_l)_{l \in \mathbb{N}}\) converges (strongly) to \(x \in X\) if
\[\begin{equation} \lim_{l \rightarrow \infty} \norm{x_l - x}_X = 0. \end{equation}\]It can be seen that the strong convergence is just the convergence with respect to the “distance between points”, or more generally, the so-called “norm” defined for a linear space, which is what we have been familiar with in fundamental calculus.
-
Definition (Weak convergence) Let \(X\) be a Banach space and \(X'\) be its dual space. The sequence \((x_l)_{l \in \mathbb{N}}\) in \(X\) converges weakly to \(x \in X\) if
\[\begin{equation} \lim_{l \rightarrow \infty} \abs{f(x_l) - f(x)} = 0 \quad (\forall f \in X'). \end{equation}\]We can see that the convergence here is called weak, because it is not directly based on point distance in the original space \(X\), but the evaluation of an arbitrary functional in the dual space on the sequence.
It is easy and natural to see that the strong convergence implies weak convergence because of the continuity of the linear functional \(f \in X'\):
\[\begin{equation} \abs{f(x_l) - f(x)} = \abs{f(x_l - x)} \leq \norm{f}_{X'} \norm{x_l - x}_X. \end{equation}\] -
Definition (Pointwise convergence) Let \(X\) and \(Y\) be normed spaces. The sequence of bounded linear operators \((T_l)_{l \in \mathbb{N}} \subset L(X, Y)\) converges to \(T \in L(X, Y)\) if
\[\begin{equation} \lim_{l \rightarrow \infty} \norm{T_l x - T x}_Y = 0 \quad (\forall x \in X). \end{equation}\]The pointwise convergence is used to describe the convergence of operators at each point in \(X\). A more strict convergence for operators is uniform convergence, which means the convergence speeds of \((T_l x)_{l \in \mathbb{N}}\) at different points \(x\) in \(X\) are comparable. It is also easy to see that the strong convergence of \((T_l)_{l \in \mathbb{N}}\) implies pointwise convergence:
\[\begin{equation} \lVert T_lx - Tx \rVert_Y = \lVert (T_l - T)x \rVert_Y \leq \lVert T_l - T \rVert_{L(X,Y)} \lVert x \rVert_X. \end{equation}\] -
Definition (Weak-* convergence) Let \(X_s'\) be the strong dual space of the normed linear space \(X\). The linear functional sequence \((T_l)_{l \in \mathbb{N}}\) converges to \(T\) in \(X_s'\) if
\[\begin{equation} \lim_{l \rightarrow \infty} \abs{T_l x - T x} = 0 \quad (\forall x \in X). \end{equation}\]The weak-* convergence can be considered as a special case of pointwise convergence with the difference that the linear operators become linear functionals and the dual space \(X'\) of \(X\) is assigned with the strong topology.