Voltage distribution simulation using 3D Galerkin BEM

今日完成混合边界条件下 spanner model 的求解。模型规模为 35796 个单元，求解时间为 56758.6 秒，大约 15 个半小时。

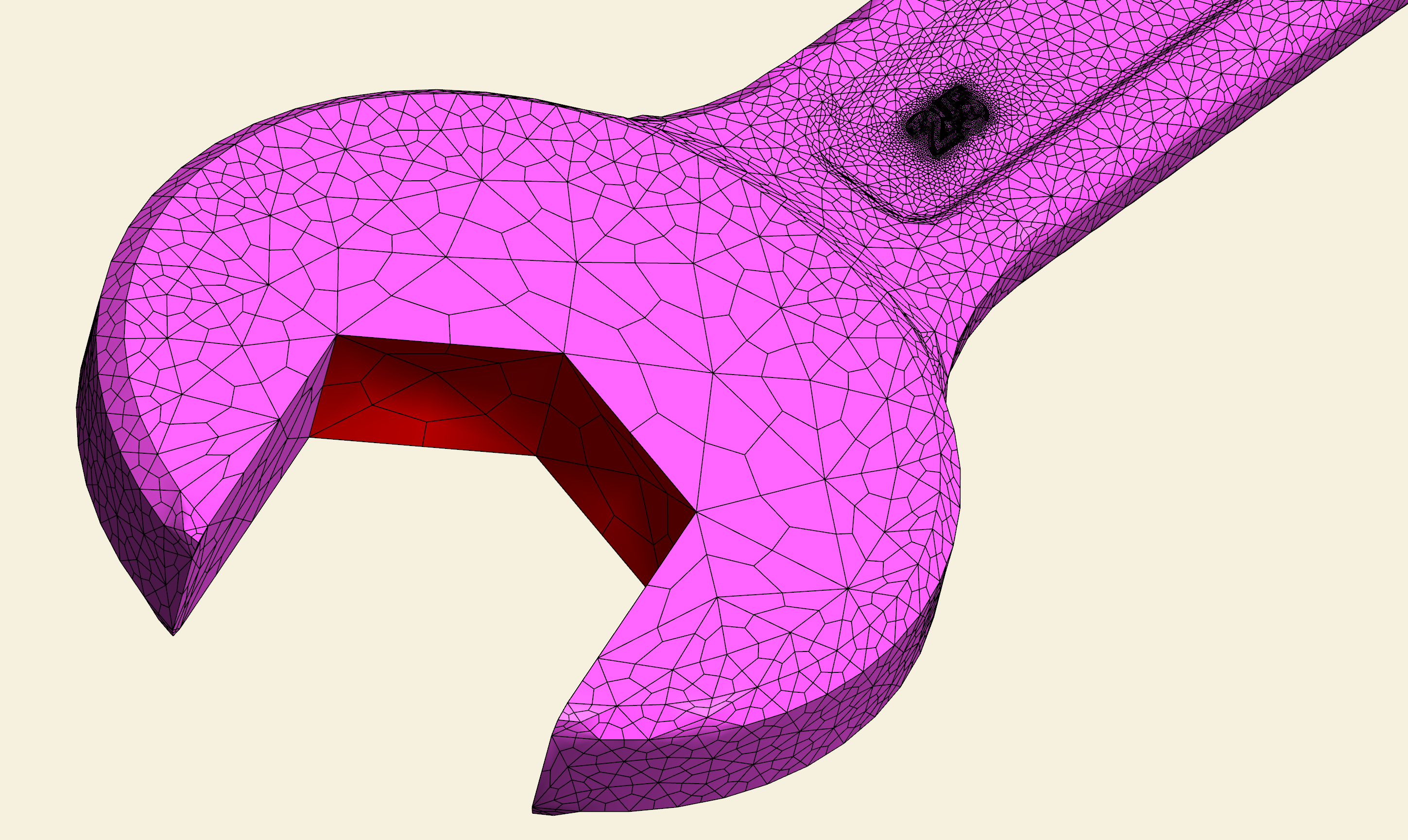
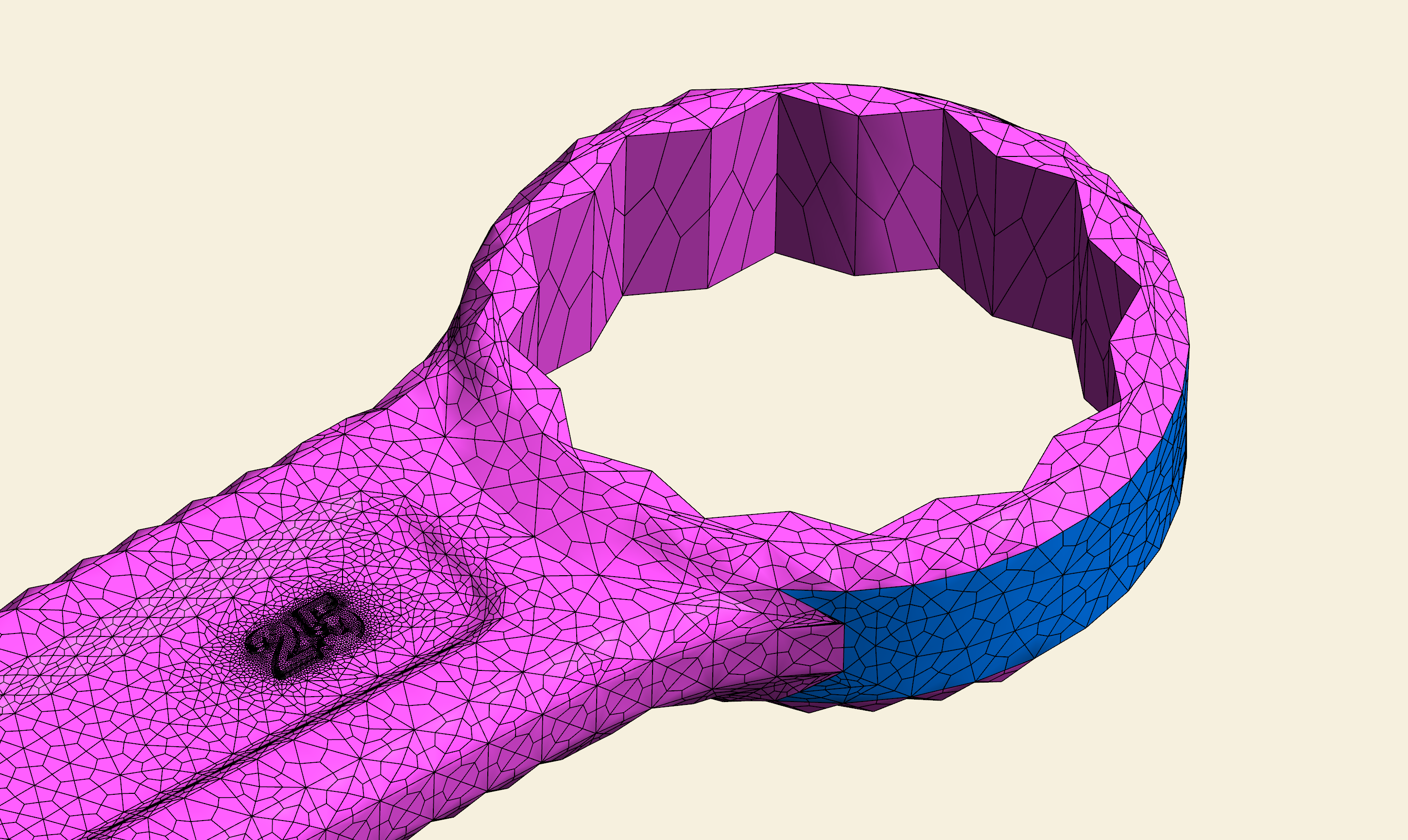
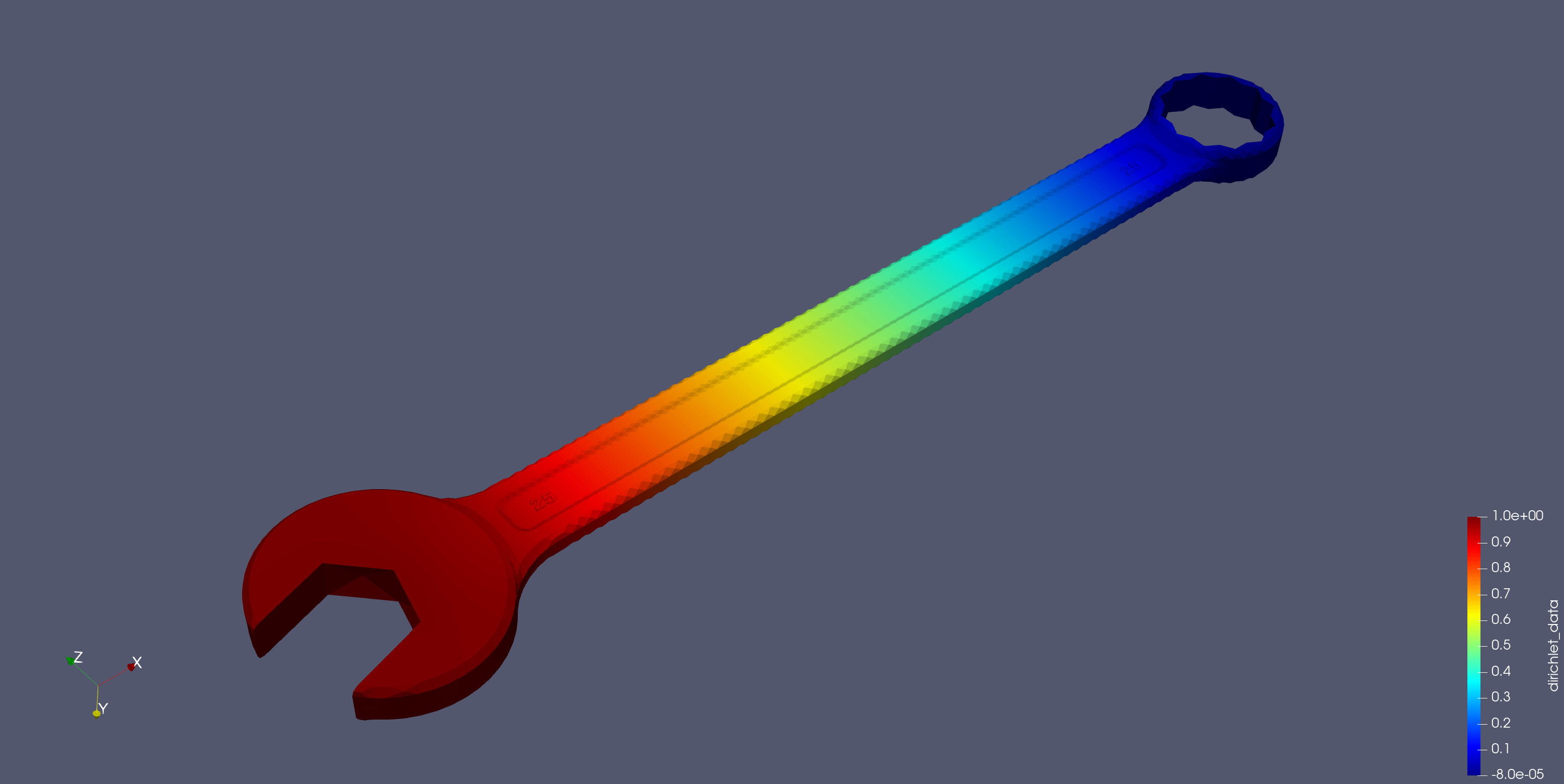
在去年 12 月份，我已初步实现了求解混合边界条件下 Laplace 方程的三维伽辽金边界元算法。那个时候曾尝试求解该模型，程序徘徊于矩阵的构建长达五天时间，都未能进入到方程的求解阶段。今年以来通过学习、实践、应用 CUDA 编程技术，终于在今天收获上述结果。整个计算过程中，内存占用量在 13 GB，左右，并未超过我的服务器 16 GB 的总内存。

若再回溯到 2020 年 10 月项目初期，那时我使用了 GNU Octave 对奇异数值积分与基于满阵的边界元方程进行求解。仅仅是 200 多个单元的模型也要计算一个多小时。而当单元数增加到 2000 左右时， Octave 脚本运行了一个多星期，导致整个机器卡死，也未得到任何结果。由此看来，对于有限元、边界元这种内存用量大、计算密集型的算法，除了对个别理论公式做解析性的推导、验证，否则从一开始就要远离 Octave 、 Python 这样的脚本语言。

虽然目前的算法性能仍不能令人满意，但它就像一颗可以不断生长、壮大的种子，让我拥有一个能够持续改进与提升的平台，有了一个可以书写后续故事的起点。根据程序运行过程中的观察，矩阵计算耗费的时间依旧很长，需要做细致的性能分析，找出瓶颈；严谨、合理地使用 GPU 的多级内存；使用性能更好的计算机设备，将计算的压力从软件转移至硬件。这样一来，就可以形成通用算法、高度并行化设计与强大的并行计算硬件三者结合的技术路线，在软件层面的抽象设计与工程层面的高性能需求间找到平衡点。