Metaphor of quotient space
In James Munkres “Topology” Section 22, the quotient space is defined as below.
Definition Let \(X\) be a topological space, and let \(X^*\) be a partition of \(X\) into disjoint subsets whose union is \(X\). Let \(p: X \rightarrow X^*\) be the surjective map that carries each point of \(X\) to the element of \(X^*\) containing it. In the quotient topology induced by \(p\), the space \(X^*\) is called a quotient space of \(X\).
The key factors in this definition are:
- According to section 3, the quotient space \(X^*\) as a partition of \(X\) is associated with a unique equivalence relation on \(X\). This equivalence relation specifies which points in the original space \(X\) will be treated as a same point in the new space \(X^*\).
- The quotient map \(p: X \rightarrow X^*\) for constructing the quotient topology on \(X^*\) introduces the concept of saturated sets, which are pre-images of subsets in \(X^*\). \(p\) ensures the image of any saturated open/closed set in \(X\) is still open/closed in \(X^*\).
With these concepts in mind, we can take paper folding and pasting as an example. Let the space \(X\) be a piece of paper. The equivalence classes on \(X\) determine which parts of this piece of paper will be pasted together. Meanwhile, the quotient map \(p\) collects the neighborhoods around every points in \(X\) that are to be pasted into a common point \(x_0\) in \(X^*\) and builds up a new neighborhood of \(x_0\) in \(X^*\). The neighborhoods of points in \(X\) are defined with respect to the subspace topology on \(X\), which is induced from the standard topology on \(\mathbb{R}^2\). The neighborhoods of points in \(X^*\) are defined with respect to the quotient topology on \(X^*\). That the quotient map \(p\) is surjective implies the whole paper is kept during the operations without cutting off any part. Hence, the obtained quotient space \(X^*\) is just the piece of paper after these folding and pasting operations. The following figure illustrates the above metaphor of quotient space by folding a piece of rectangular paper into a cylinder.
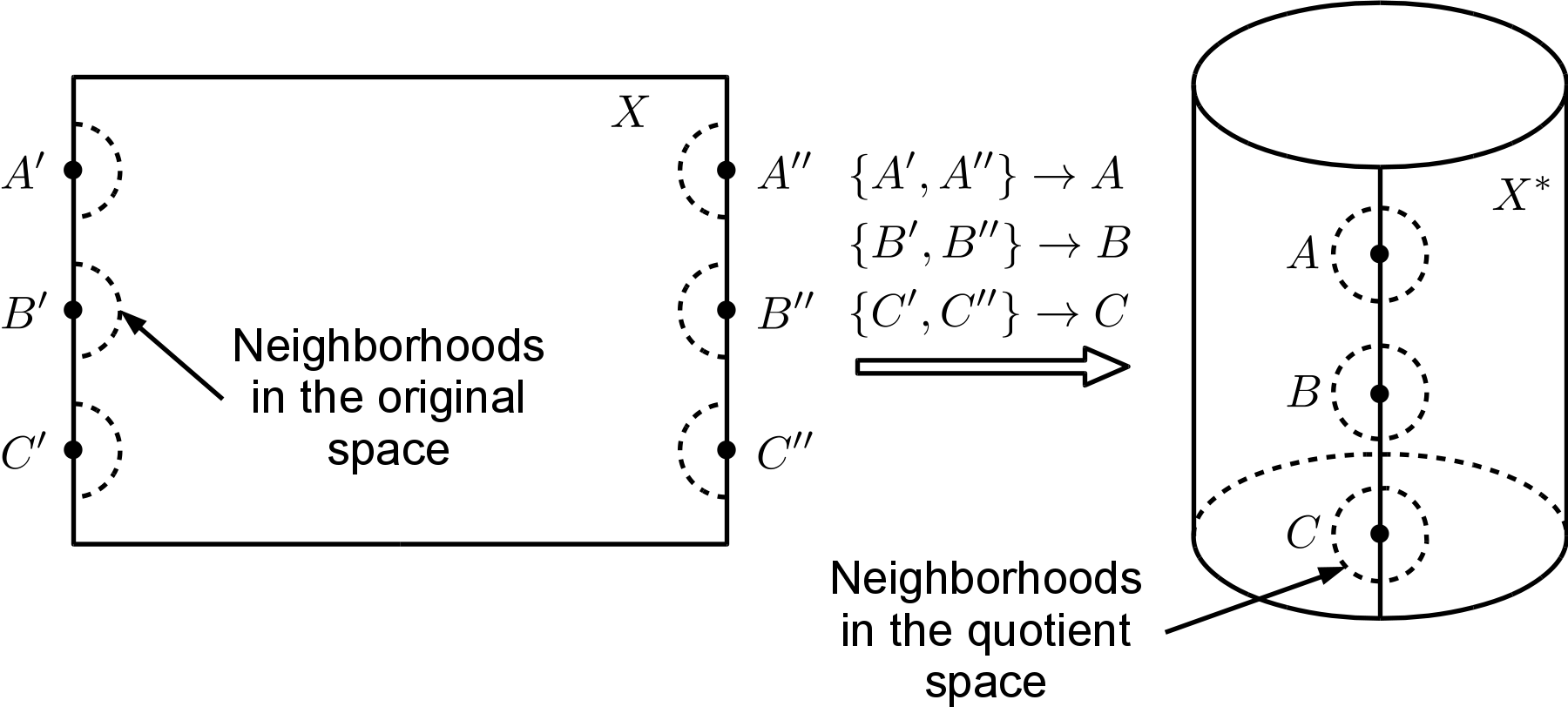
Figure. Illustration of quotient space using the example of paper folding and pasting.