Understanding of continuity definition in topology
When we learn calculus in university as freshmen, we are usually force-fed with the \(\epsilon-\delta\) language for the definition of a function’s continuity, i.e.
A function \(f: A \rightarrow \mathbb{R}\) with \(A \subseteq \mathbb{R}\) as its domain is continuous at \(x_0 \in A\) if for all \(\epsilon > 0\), there exists a \(\delta > 0\) such that whenever \(x \in A\) and \(\left\vert x - x_0 \right\vert < \delta\), there is \(\vert f(x) - f(x_0) \vert < \epsilon\).
Although the abstract and formal \(\epsilon-\delta\) language is not easy to get used to at first, the idea embodied in the definition is obvious: any small amount of deviation or error around \(f(x_0)\) is procurable by making a corresponding perturbation about \(x_0\), so that the function does not have significant jump at \(x_0\) and is thus considered to be continuous.
In topology, the definition of continuity is based on open sets, which is more abstract compared to the above tangible version, i.e.
Let \(X\) and \(Y\) be topological spaces. \(f: X \rightarrow Y\) is a continuous function if for all open set \(V\) in \(Y\), its pre-image \(U = f^{-1}(V)\) is open in \(X\). For a point \(x_0 \in X\) and each neighborhood \(V\) of \(f(x_0)\), there is a neighborhood \(U\) of \(x_0\) such that \(f(U) \subset V\), we say the function is continuous at \(x_0\).
At first glance, this definition seems merely a product of a mathematician’s endowment, which just works and needs no psychological acceptance. However, it is never a good luck by chance, but requires an understanding with profundity and discernment, which explores the topological essence underpinning the metric space \(\mathbb{R}\).
Take the definition of sequence convergence as an analogy. Its definition in the normal metric space \(\mathbb{R}\), which we are familiar with, is based on the absolute value of real numbers for measuring point proximity, while its definition in a general topological space involves only point inclusion in open sets, i.e.
Let \(X\) be a topological space and \(\{x_n\}_{n \geq 1}\) be a sequence in \(X\). We say \(\{x_n\}_{n \geq 1}\) converges to a point \(x_0\) in \(X\) if for any neighborhood \(U\) of \(x_0\), there exists a \(N\) in \(\mathbb{Z}_+\), such that when \(n > N\), \(x_n\) belongs to \(U\).
From this it can be seen that the notion of metric or distance is discarded in the topological space, where the rulers for measuring point proximity degenerates to a collection of open sets. Because set inclusion relation establishes a partial order on this open set collection, the meaning of metric or distance is still kept to some extent. Assume that we select a collection of nested open sets (forming a chain in the order relation) as rulers to measure point convergence. The smaller the open set used to circumscribe a segment of the sequence \(\{x_n\}_{n \geq 1}\), the closer they approach the limiting point \(x_0\). This concept is illustrated below.
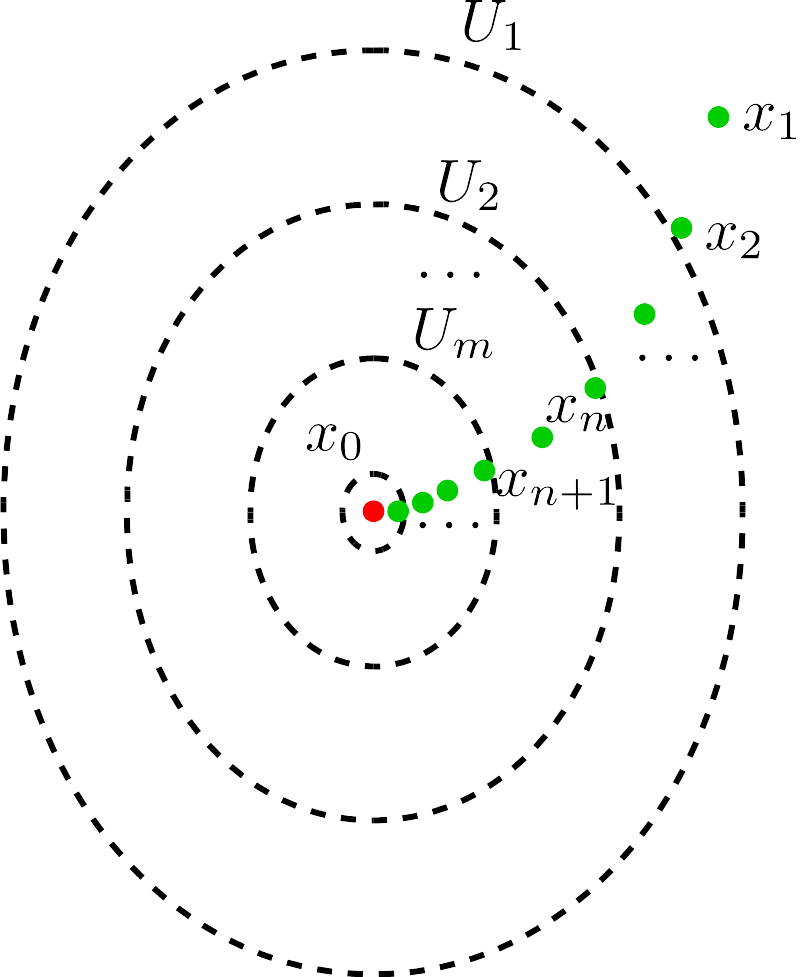
Fig. Convergence of a sequence of points in topological space.
Similarly, for the definition of function continuity in pure topological spaces, the only tool for measuring the amount of deviation or error about a point \(x_0\) and its function value \(f(x_0)\) is using open sets. The smaller the open set, the finer the measuring resolution. If the function value can be limited within any neighborhood of \(f(x_0)\) by confining the variation of \(x\) around \(x_0\) in \(X\), we can say that the set of rulers selected from \(Y\), viz. its topology, has tried its best to ensure the function’s continuity at \(x_0\). It is easy to project that the finer the topology of \(Y\), the more difficult the function to be continuous, due to the improved resolution of the rulers.
Then, looking back at the definition of function continuity in metric space \(\mathbb{R}\), the basis elements of its topology can be infinitesimally small, i.e. \((a, b)\) can have a length approaching zero. Therefore, the continuous functions we meet in college calculus are actually defined in a very strict sense and it’s no doubt that they exhibit elegant silhouettes. Meanwhile, we also see that the continuity of a function not only relies on its rule of assignment, but also on the adopted topologies.
Equivalence between the two definitions
After clarifying the concepts of function continuity, we will show the equivalence between its two definitions, the \(\epsilon-\delta\) version and the open set version.
Open set version \(\Longrightarrow\) \(\epsilon-\delta\) version
Let \(y = f(x)\) and \(y_0 = f(x_0)\). The condition \(\vert y - y_0 \vert < \epsilon\) forms an open interval in \(Y = \mathbb{R}\), i.e. \((y_0 - \epsilon, y_0 + \epsilon)\) for any \(\epsilon > 0\), which is a basis element of the metric topology on \(Y\) (and also of its order topology). Then, according to the open set version, \(f^{-1} ((y_0 - \epsilon, y_0 + \epsilon))\) is open in \(X\). Because \(y_0 \in (y_0 - \epsilon, y_0 + \epsilon)\), \(x_0 \in f^{-1}((y_0 - \epsilon, y_0 + \epsilon))\). Then there exists a basis element \((a, b)\) around \(x_0\), such that \((a, b) \subset f^{-1}((y_0 - \epsilon, y_0 + \epsilon))\). By letting \(\delta = \min\{x_0 - a, b - x_0\}\), we have \(x \in (x_0 - \delta, x_0 + \delta)\), i.e. \(\vert x - x_0 \vert < \delta\) ensuring \(\vert y - y_0 \vert < \epsilon\).
\(\epsilon-\delta\) version \(\Longrightarrow\) open set version
Let \(V\) be an open set in \(Y = \mathbb{R}\) assigned with the metric topology.Then for all \(y_0 \in V\), there exists an open interval \((c, d)\) containing \(y_0\), such that \((c, d) \subset V\). Let \(\epsilon = \min\{y_0 - c, d - y_0\}\), we have \(y_0 \in (y_0 - \epsilon, y_0 + \epsilon) \subset V\). According to the given \(\epsilon-\delta\) version, there exists a \(\delta > 0\) such that when \({\rm dist}_X (x, x_0) = \vert x - x_0 \vert < \delta\), \({\rm dist}_Y(y, y_0) = \vert y - y_0 \vert < \epsilon\). It should be noted here that because \(f\) may not be injective, there could be more than one element in \(f^{-1}(y_0)\). Then the above \(\epsilon-\delta\) condition holds for any \(x_0\) selected from \(f^{-1}(y_0)\).
Because \(y_0\) is arbitrary in \(V\) and \(x_0\) is arbitrary in \(f^{-1}(y_0)\), taking the union of all such open intervals \((x_0 - \delta, x_0 + \delta)\) will produce \(f^{-1}(V)\), which is also an open set in \(X\).