Build a block cluster tree

In our previous example, we have learnt how to build a cluster tree for all the DoFs held within a DoF handler, which is associated with a finite element and a triangulation. We also know that to build an $\mathcal{H}$-matrix as a finite dimensional approximation of a bilinear form $b_A: X\times Y' \rightarrow \mathbb{R}$ induced from the boundary integral operator $A: X \rightarrow Y$, a block cluster tree should be constructed from two cluster trees: one for the finite dimensional test space $Y_h'$ and the other for the finite dimensional trial space $X_h$. In this example, we will demonstrate to how to build this block cluster tree.

Let $J$ and $I$ be the DoF index sets for the two spaces $X_h$ and $Y_h'$. The two cluster trees are represented as $T(J)$ and $T(I)$. The block cluster tree built from them is $T(I\times J)$. The DoF index sets of the leaf nodes of $T(J)$ forms a partition of the complete DoF index set $J$. Then if $u$ is a vector in $X_h$, it can be partitioned into a block vector. In a same way, a vector $v$ in $Y_h'$ can be partitioned into a block vector according to the leaf nodes of $T(I)$. Similarly, if $\mathcal{A}$ is a matrix mapping from $X_h$ to $Y_h'$, it can be partitioned into matrix blocks with respect to the leaf nodes of the block cluster tree $T(I\times J)$.

The block cluster tree $T(I\times J)$ is a quad tree, which can be constructed in a recursive fashion as below.

The block cluster $I\times J$ is the root node of $T(I\times J)$.
Starting from the root node, recursively partition the current node according to the following cases.

Assume the current node is $\tau\times\sigma$, where $\tau$ is a cluster in $T(I)$ and $\sigma$ is a cluster in $T(J)$.
- If either $\tau$ or $\sigma$ is a leaf node of their respective cluster tree, $\tau\times\sigma$ is a near-field leaf node of $T(I\times J)$.
- If $\tau$ and $\sigma$ satisfy one of the following $\eta$-admissibility conditions,
  \[\begin{equation} \label{eq:admissibility-condition} \begin{aligned} \diam(\supp(\tau)) &\leq \eta \dist(\supp(\tau),\supp(\sigma)) \\ \diam(\supp(\sigma)) &\leq \eta \dist(\supp(\tau),\supp(\sigma)) \\ \min \{ \diam(\supp(\tau)), \diam(\supp(\sigma)) \} &\leq \eta \dist(\supp(\tau),\supp(\sigma)) \\ \max \{ \diam(\supp(\tau)), \diam(\supp(\sigma)) \} &\leq \eta \dist(\supp(\tau),\supp(\sigma)) \end{aligned}, \end{equation}\]
  $\tau\times\sigma$ is a far-field leaf node of $T(I\times J)$. $\eta > 0$ is the admissibility constant. In HierBEM, the third $\eta$-admissibility condition is adopted.
  
  Here $\supp$ returns the union of support sets of basis functions related with its input cluster. We can consider this union as the support of the cluster. $\diam$ returns the diameter of a cluster’s support. $\dist$ returns the minimum distance between the supports of two input clusters. It is easy to see that if $\eta$ increases, it is more likely for two givens clusters to be admissible.
  
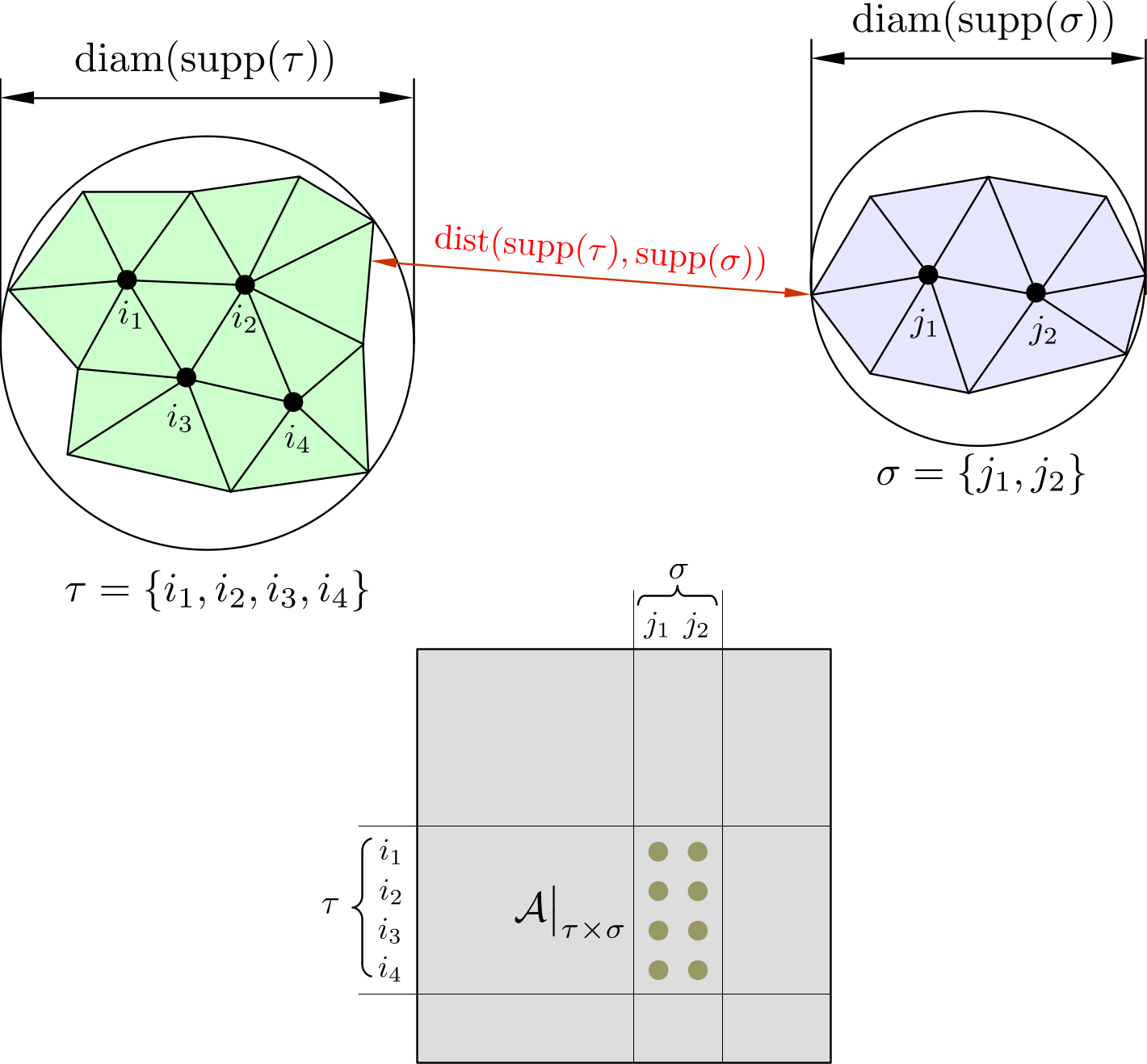
  The following figure shows the DoF support points in the two clusters $\tau$ and $\sigma$, their support sets and the corresponding matrix block $\mathcal{A}\big\vert_{\tau\times\sigma}$.
- If the above two cases are not satisfied, the two clusters $\tau$ and $\sigma$ are not leaf nodes. Their sons are $S(\tau) = \{\tau_1,\tau_2 \}$ and $S(\sigma) = \{\sigma_1, \sigma_2 \}$, where $S$ is a function returning the set of sons of the input cluster or block cluster. Then the sons of the block cluster $\tau\times\sigma$ are constructed by taking the tensor product of $S(\tau)$ and $S(\sigma)$:
  \[\begin{equation} S(\tau\times\sigma) = \{ \tau_1\times\sigma_1,\tau_1\times\sigma_2,\tau_2\times\sigma_1,\tau_2\times\sigma_2 \}. \end{equation}\]

The constructed block cluster tree $T(I\times J)$ is level conserving, which means the level of a node $\tau\times\sigma$ in the block cluster tree is equal to the level of $\tau$ in $T(I)$ and the level of $\sigma$ in $T(J)$, i.e.

\[\begin{equation} \mathrm{level}(\tau\times\sigma) = \mathrm{level}(\tau) = \mathrm{level}(\sigma). \end{equation}\]

In HierBEM, all block cluster trees are level conserving.

With the above concepts clarified, we can now go through the source code in hierbem/examples/build-block-cluster-tree/build-block-cluster-tree.cc.

We include the following header files and import namespaces.

#include <deal.II/base/exceptions.h>
#include <deal.II/base/point.h>
#include <deal.II/base/types.h>

#include <deal.II/dofs/dof_handler.h>
#include <deal.II/dofs/dof_tools.h>

#include <deal.II/fe/fe_dgq.h>
#include <deal.II/fe/fe_q.h>
#include <deal.II/fe/mapping.h>
#include <deal.II/fe/mapping_q.h>

#include <deal.II/grid/grid_generator.h>
#include <deal.II/grid/tria.h>

#include <fstream>
#include <iostream>
#include <memory>
#include <vector>

#include "cluster_tree/block_cluster_tree.h"
#include "cluster_tree/cluster_tree.h"
#include "dofs/dof_tools_ext.h"

using namespace HierBEM;
using namespace dealii;

We define a builder class for constructing a cluster tree. Its constructor needs a mapping object and a DoF handler to get the coordinates of support points as well as the average cell size at these points. The member function build constructs the cluster tree and returns its smart pointer. The smart pointer being unique_ptr is because a cluster tree will only be owned with a unique function space.

template <int spacedim>
class ClusterTreeBuilder
{
public:
  template <int dim>
  ClusterTreeBuilder(const Mapping<dim, spacedim>    &mapping,
                     const DoFHandler<dim, spacedim> &dof_handler,
                     const unsigned int               _n_min);

  std::unique_ptr<ClusterTree<spacedim>>
  build() const;

  std::vector<Point<spacedim>> &
  get_support_points()
  {
    return support_points;
  }

  const std::vector<Point<spacedim>> &
  get_support_points() const
  {
    return support_points;
  }

  std::vector<double> &
  get_dof_average_cell_size()
  {
    return dof_average_cell_size;
  }

  const std::vector<double> &
  get_dof_average_cell_size() const
  {
    return dof_average_cell_size;
  }

private:
  std::vector<Point<spacedim>> support_points;
  std::vector<types::global_dof_index> dof_indices;
  std::vector<double> dof_average_cell_size;
  unsigned int n_min;
};

Next, we define a class BEMFunctionSpace, which encapsulates a DoF handler, a cluster tree and a cluster tree builder.

template <int dim, int spacedim>
class BEMFunctionSpace
{
public:
  BEMFunctionSpace(const DoFHandler<dim, spacedim> &dof_handler_,
                   const Mapping<dim, spacedim>    &mapping,
                   const unsigned int               n_min);

  ClusterTree<spacedim> &
  get_cluster_tree()
  {
    return *cluster_tree;
  }

  const ClusterTree<spacedim> &
  get_cluster_tree() const
  {
    return *cluster_tree;
  }

  ClusterTreeBuilder<spacedim> &
  get_cluster_tree_builder()
  {
    return *cluster_tree_builder;
  }

  const ClusterTreeBuilder<spacedim> &
  get_cluster_tree_builder() const
  {
    return *cluster_tree_builder;
  }

  std::vector<Point<spacedim>> &
  get_support_points()
  {
    return cluster_tree_builder->get_support_points();
  }

  const std::vector<Point<spacedim>> &
  get_support_points() const
  {
    return cluster_tree_builder->get_support_points();
  }

  std::vector<double> &
  get_dof_average_cell_size()
  {
    return cluster_tree_builder->get_dof_average_cell_size();
  }

  const std::vector<double> &
  get_dof_average_cell_size() const
  {
    return cluster_tree_builder->get_dof_average_cell_size();
  }

  std::vector<types::global_dof_index> &
  get_internal_to_external_dof_numbering()
  {
    return cluster_tree->get_internal_to_external_dof_numbering();
  }

  const std::vector<types::global_dof_index> &
  get_internal_to_external_dof_numbering() const
  {
    return cluster_tree->get_internal_to_external_dof_numbering();
  }

  std::vector<types::global_dof_index> &
  get_external_to_internal_dof_numbering()
  {
    return cluster_tree->get_external_to_internal_dof_numbering();
  }

  const std::vector<types::global_dof_index> &
  get_external_to_internal_dof_numbering() const
  {
    return cluster_tree->get_external_to_internal_dof_numbering();
  }

private:
  const DoFHandler<dim, spacedim>              &dof_handler;
  std::unique_ptr<ClusterTree<spacedim>>        cluster_tree;
  std::unique_ptr<ClusterTreeBuilder<spacedim>> cluster_tree_builder;
};

Then we can use a boundary integral kernel function, two function spaces, one is the test space and the other is the trial space, to define a bilinear form. Because in this example we only demonstrate how to construct a block cluster tree, the bounday integral kernel function is omitted in the bilinear form definition. In the constructor of BEMBilinearForm, the trial space argument appears before the test space argument, which is consistent with the mathematical definition of a bilinear form $b_A: X\times Y' \rightarrow \mathbb{R}$.

template <int dim, int spacedim>
class BEMBilinearForm
{
public:
  BEMBilinearForm(const BEMFunctionSpace<dim, spacedim> &trial_space_,
                  const BEMFunctionSpace<dim, spacedim> &test_space_);

  void
  build_block_cluster_tree(const double eta, const unsigned int n_min);

  ClusterTree<spacedim> &
  get_cluster_tree_trial_space()
  {
    return trial_space.get_cluster_tree();
  }

  const ClusterTree<spacedim> &
  get_cluster_tree_trial_space() const
  {
    return trial_space.get_cluster_tree();
  }

  ClusterTree<spacedim> &
  get_cluster_tree_test_space()
  {
    return test_space.get_cluster_tree();
  }

  const ClusterTree<spacedim> &
  get_cluster_tree_test_space() const
  {
    return test_space.get_cluster_tree();
  }

  BlockClusterTree<spacedim> &
  get_block_cluster_tree()
  {
    return *block_cluster_tree;
  }

  const BlockClusterTree<spacedim> &
  get_block_cluster_tree() const
  {
    return *block_cluster_tree;
  }

private:
  const BEMFunctionSpace<dim, spacedim>      &trial_space;
  const BEMFunctionSpace<dim, spacedim>      &test_space;
  std::unique_ptr<BlockClusterTree<spacedim>> block_cluster_tree;
};

The member function build_block_cluster_tree for constructing a block cluster tree from the two cluster trees is as below. The n_min argument can be different from the n_min used for building $T(I)$ or $T(J)$. In the constructor of BlockClusterTree, the test space argument appears before the trial space argument, since the former is related to matrix rows, while the latter is related to matrix columns. This is consistent with how we specify the dimensions of a matrix, where the row dimension appears before the column dimension.

template <int dim, int spacedim>
void
BEMBilinearForm<dim, spacedim>::build_block_cluster_tree(
  const double       eta,
  const unsigned int n_min)
{
  block_cluster_tree = std::make_unique<BlockClusterTree<spacedim>>(
    test_space.get_cluster_tree(), trial_space.get_cluster_tree(), eta, n_min);
  block_cluster_tree->partition(
    test_space.get_internal_to_external_dof_numbering(),
    trial_space.get_internal_to_external_dof_numbering(),
    test_space.get_support_points(),
    trial_space.get_support_points(),
    test_space.get_dof_average_cell_size(),
    trial_space.get_dof_average_cell_size());
}

Now we come to the main function. At first, we create a triangulation for a unit sphere as before. Only one global refinement is performed, so that the block cluster tree will not be too large and inconvenient for visualization.

const unsigned int    dim      = 2;
const unsigned int    spacedim = 3;
const Point<spacedim> center(0, 0, 0);
const double          radius(1);
const unsigned int    refinement = 1;

Triangulation<dim, spacedim> tria;
GridGenerator::hyper_sphere(tria, center, radius);
tria.refine_global(refinement);

After creating a second order mapping object, we create two function spaces to approximate Sobolev spaces $H^{1/2}(\Gamma)$ and $H^{-1/2}(\Gamma)$. For $H^{1/2}(\Gamma)$, we use the continuous first order Lagrange finite element FE_Q(1). For $H^{-1/2}(\Gamma)$, we use the piecewise constant finite element FE_DGQ(0).

const unsigned int        fe_H_half_order = 1;
  FE_Q<dim, spacedim>       fe_H_half(fe_H_half_order);
  DoFHandler<dim, spacedim> dof_handler_H_half(tria);
  dof_handler_H_half.distribute_dofs(fe_H_half);
  BEMFunctionSpace<dim, spacedim> H_half(dof_handler_H_half,
                                         mapping,
                                         n_min_H_half);

const unsigned int        fe_H_minus_half_order = 0;
  FE_DGQ<dim, spacedim>     fe_H_minus_half(fe_H_minus_half_order);
  DoFHandler<dim, spacedim> dof_handler_H_minus_half(tria);
  dof_handler_H_minus_half.distribute_dofs(fe_H_minus_half);
  BEMFunctionSpace<dim, spacedim> H_minus_half(dof_handler_H_minus_half,
                                               mapping,
                                               n_min_H_minus_half);

With these two function spaces, we create a BEMBilinearForm object with its block cluster tree for the bilinear form of the single layer potential operator $b_V: H^{-1/2}(\Gamma)\times H^{-1/2}(\Gamma) \rightarrow \mathbb{R}$, and another one for the bilinear form of the double layer potential operator $b_K: H^{1/2}(\Gamma)\times H^{-1/2}(\Gamma) \rightarrow \mathbb{R}$.

BEMBilinearForm<dim, spacedim> bV(H_minus_half, H_minus_half);
bV.build_block_cluster_tree(eta, n_min_block_cluster_tree);
BEMBilinearForm<dim, spacedim> bK(H_minus_half, H_half);
bK.build_block_cluster_tree(eta, n_min_block_cluster_tree);

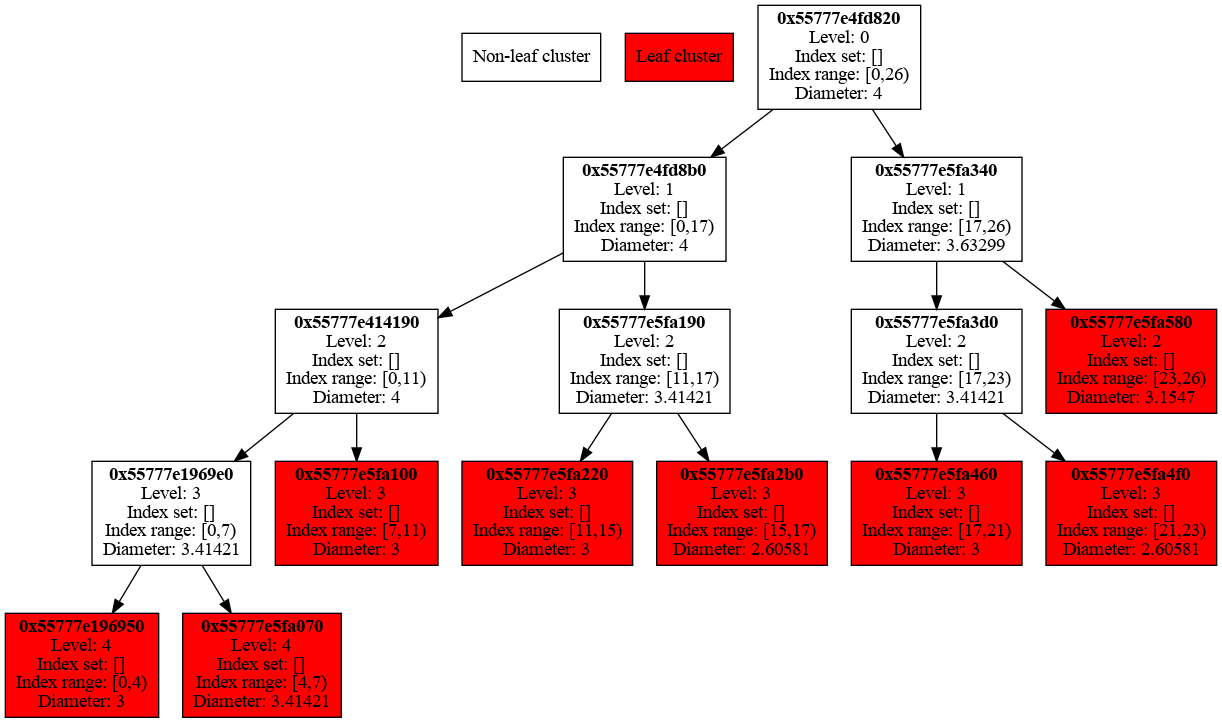
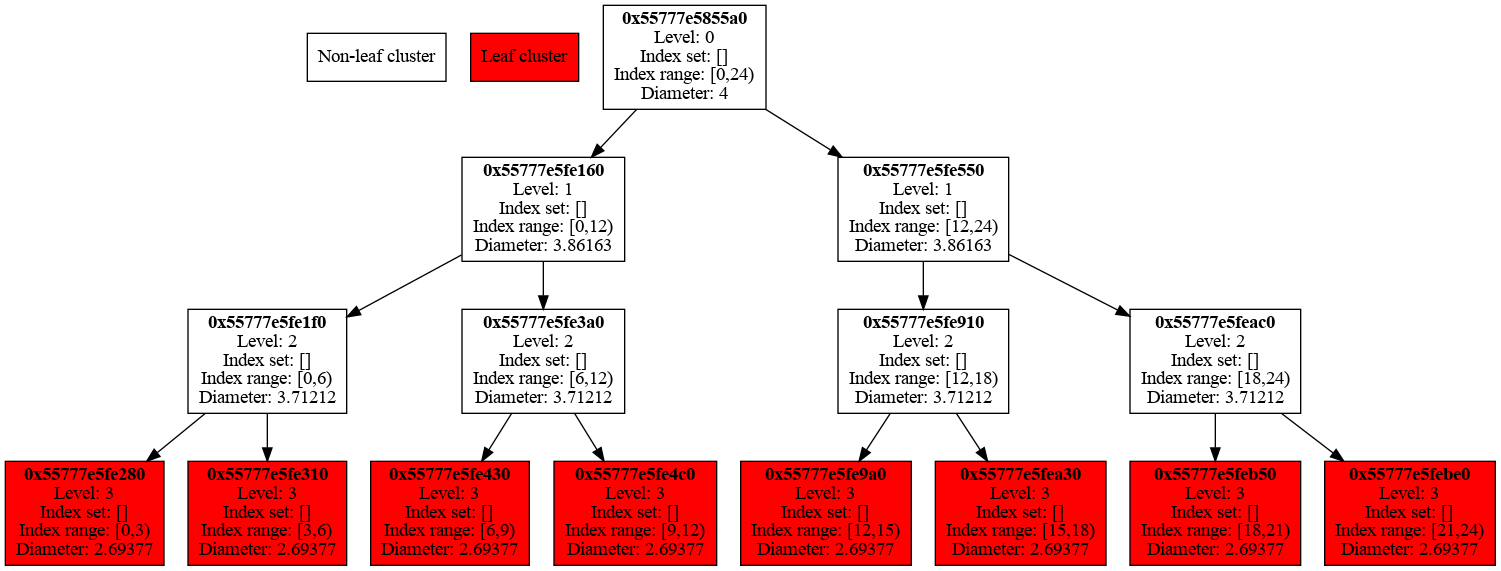
Finally, we export directed graphs of the cluster trees for the two function spaces as well as graphs of the two block cluster trees for the two bilinear forms.

std::ofstream graph("cluster-tree-H-half.puml");
H_half.get_cluster_tree().print_tree_info_as_dot(graph);
graph.close();

graph.open("cluster-tree-H-minus-half.puml");
H_minus_half.get_cluster_tree().print_tree_info_as_dot(graph);
graph.close();

// Print out the block cluster trees for the two bilinear forms.
graph.open("bV-block-cluster-tree.puml");
bV.get_block_cluster_tree().print_bct_info_as_dot(graph);
graph.close();

graph.open("bK-block-cluster-tree.puml");
bK.get_block_cluster_tree().print_bct_info_as_dot(graph);
graph.close();

After running the example, we process these files with PlantUML on the command line and obtain the following graph images.

find . -name "*.puml" -exec plantuml {} \;

$Cluster tree for the function space $$H^{1/2}(\Gamma) $$.$

$Cluster tree for the function space $$H^{-1/2}(\Gamma) $$.$